题目内容
(15分)在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上(如图),且OC=1,OA=a+1(a>1),点D在边OA上,满足OD=a. 分别以OD、OC为长、短半轴的椭圆在矩形及其内部的部分为椭圆弧CD. 直线l:y=-x+b与椭圆弧相切,与AB交于点E.
(1)求证:![]() ;
;
(2)设直线l将矩形OABC分成面积相等的两部分,求直线l的方程;
(3)在(2)的条件下,设圆M在矩形及其内部,且与l和线段EA都相切,求面积最大的圆M的方程.

解析:题设椭圆的方程为![]() . …………………………1分
. …………………………1分
由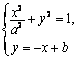 消去y得
消去y得![]() . ………………………2分
. ………………………2分
由于直线l与椭圆相切,故△=(-2a2b)2-4a2(1+a2) (b2-1)=0,
化简得![]() . ① …………………………4分
. ① …………………………4分
(2)由题意知A(a+1,0),B(a+1,1),C(0,1),
于是OB的中点为![]() . ………………………5分
. ………………………5分
因为l将矩形OABC分成面积相等的两部分,所以l过点![]() ,
,
即![]() ,亦即
,亦即![]() . ② …………………………6分
. ② …………………………6分
由①②解得![]() ,故直线l的方程为
,故直线l的方程为![]() ………………………8分
………………………8分
(3)由(2)知![]() .
.
因为圆M与线段EA相切,所以可设其方程为![]() .………9分
.………9分
因为圆M在矩形及其内部,所以 ④ ……………………… 10分
④ ……………………… 10分
圆M与 l相切,且圆M在l上方,所以![]() ,即
,即![]() .
.
………………………12分
代入④得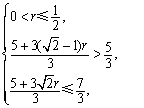 即
即![]() ………………………13分
………………………13分
所以圆M面积最大时,![]() ,这时,
,这时,![]() .
.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是