题目内容
已知函数f(x)=3x+2,x∈[-1,2],证明该函数的单调性并求出其最大值和最小值.
【答案】
见解析。最小值是-1,最大值是8.
【解析】利用函数的单调性的定义证明来证明单调性,第一步取值(在所证区间取两个不同的值),第二步作差比较函数值差的符合,第三步得出结论.
设x1,x2是区间[-1,2]上的任意两个实数,且x1<x2,则
f(x1)-f(x2)=3x1+2-3x2-2=3(x1-x2).
由x1<x2,得x1-x2<0,
于是f(x1)-f(x2)<0,即f(x1)<f(x2).
所以,函数f(x)=3x+2是区间[-1,2]上的增函数.
因此,函数f(x)=3x+2在区间[-1,2]的两个端点上分别取得最小值与最大值,即在
x=-1时取得最小值,最小值是-1,在x=2时取得最大值,最大值是8.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
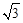 sin ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin ax cos ax+2 cos2 ax的周期为π,其中a>0. sin
ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin
ax cos ax+2 cos2 ax的周期为π,其中a>0. 的最大值;
的最大值; )>kg(x)对x∈[2,4]有解,求实数k的取值范围.
)>kg(x)对x∈[2,4]有解,求实数k的取值范围. sin
ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin
ax cos ax+2 cos2 ax的周期为π,其中a>0. ,无最小值
,无最小值