题目内容
如图4,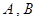 是圆
是圆 上的两点,且
上的两点,且 ,
, ,
,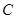 为
为 的中点,连接
的中点,连接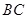 并延长交圆
并延长交圆 于点
于点 ,则
,则 .
. 
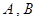 是圆
是圆 上的两点,且
上的两点,且 ,
, ,
,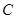 为
为 的中点,连接
的中点,连接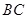 并延长交圆
并延长交圆 于点
于点 ,则
,则 .
. 
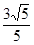
试题分析: 做AO的延长线交圆于点E,那么则根据OA=2,则OB=2,且C是AB的中点,CA=OC=1,那么根据相交弦定理,可知DC
 CB=AC
CB=AC CE,在直角三角形COB中,可知,CB=
CE,在直角三角形COB中,可知,CB=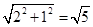 ,那么可知DC=
,那么可知DC=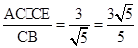 ,故答案为
,故答案为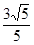 。
。点评:解决该试题的关键是做辅助线,延长AO到点E,利用相交弦定理,得到变得关系式,然后求解得到结论。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
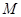 过两点
过两点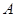 (1,-1),
(1,-1),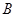 (-1,1),且圆心
(-1,1),且圆心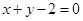 上.
上.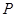 是直线
是直线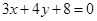 上的动点,
上的动点,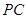 、
、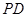 是圆
是圆 、
、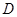 为切点,求四边形
为切点,求四边形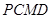 面积的最小值.
面积的最小值. 的点数共有 个。
的点数共有 个。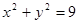 和
和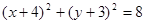 的交点的直线方程
的交点的直线方程 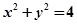 内点
内点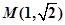 作圆的两条互相垂直的弦
作圆的两条互相垂直的弦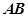 和
和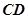 ,则
,则 的最大值为 .
的最大值为 . 

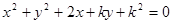 的面积最大时,圆心坐标是 ( )
的面积最大时,圆心坐标是 ( )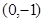
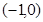
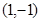
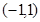
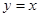 相切
相切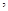 圆心在直线
圆心在直线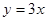 上且被
上且被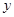 轴截得的弦长为
轴截得的弦长为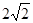 的圆的方程
的圆的方程 外一点
外一点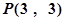 作这个圆的切线,设两条切线之间所夹的角为
作这个圆的切线,设两条切线之间所夹的角为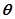 ,则
,则 .
.