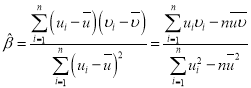题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的零点个数.
的零点个数.
(2)![]() 的最小值为
的最小值为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)见解析(2)见解析
【解析】
(1)求函数![]() 的导数,利用导数判断函数的单调性和极值,从而得到零点的个数;
的导数,利用导数判断函数的单调性和极值,从而得到零点的个数;
(2)![]() ,求导得
,求导得![]() ,可以判断
,可以判断![]() 存在零点
存在零点![]() ,可以求出函数
,可以求出函数![]() 的最小值为
的最小值为![]() ,可以证明出:
,可以证明出:
![]() ,
,![]() ,可证明
,可证明![]() 在
在![]() 上有零点,
上有零点,
![]() 的最小值为
的最小值为![]() ,结合
,结合![]() ,可求
,可求![]() 的最小值为
的最小值为![]() .
.
(1)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
①当![]() 时,
时,![]() ,
,![]() 单调递增,又
单调递增,又![]() ,
,![]() ,
,
所以函数![]() 有唯一零点;
有唯一零点;
②当![]() 时,
时,![]() 恒成立,所以函数
恒成立,所以函数![]() 无零点;
无零点;
③当![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以![]() .
.
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 无零点.
无零点.
综上所述,当![]() 时函数
时函数![]() 无零点.当
无零点.当![]() ,函数
,函数![]() 有一个零点.
有一个零点.
(2)由题意得,![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上为增函数,即
上为增函数,即![]() 在
在![]() 上为增函数.
上为增函数.
又![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上存在唯一零点
上存在唯一零点![]() ,
,
且![]() ,
,![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为减函数,当
上为减函数,当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上为增函数,
上为增函数,![]() 的最小值
的最小值![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
由![]() 得
得![]() ,易知
,易知![]() 在
在![]() 上为增函数.
上为增函数.
因为![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() 在
在
![]() 上存在唯一零点
上存在唯一零点![]() ,且
,且![]() ,
,![]() ,当
,当![]() 时,
时,
![]() ,
,![]() 在
在![]() 上为减函数,当
上为减函数,当![]() 时,
时,![]() ,
,![]() 在
在![]()
上为增函数,所以![]() 的最小值为
的最小值为![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
又函数![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() ,
,


因为![]() ,所以
,所以![]() ,即
,即![]() 在
在![]() 上的最小值为0.
上的最小值为0.

【题目】十八届五中全会首次提出了绿色发展理念,将绿色发展作为“十三五”乃至更长时期经济社会发展的一个重要理念.某地区践行“绿水青山就是金山银山”的绿色发展理念,2015年初至2019年初,该地区绿化面积y(单位:平方公里)的数据如下表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
绿化面积y | 2.8 | 3.5 | 4.3 | 4.7 | 5.2 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)利用(1)中的回归方程,预测该地区2025年初的绿化面积.
(参考公式:线性回归方程:![]() ,
,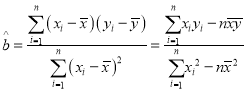 ,
,![]() 为数据平均数)
为数据平均数)
【题目】2016年1月6日北京时间上午11时30分,朝鲜中央电视台宣布“成功进行了氢弹试验”,再次震动世界,此事件也引起了我国公民热议,其中丹东市(丹东市和朝鲜隔江)某QQ聊天群有300名网友,乌鲁木齐市某微信群有200名网友,为了解不同地区我国公民对“氢弹试验”事件的关注程度,现采用分层抽样的方法,从中抽取了100名网友,先分别统计了他们在某时段发表的信息条数,再将两地网友发表的信息条数分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,分别加以统计,得到如图所示的频率分布直方图.
,分别加以统计,得到如图所示的频率分布直方图.
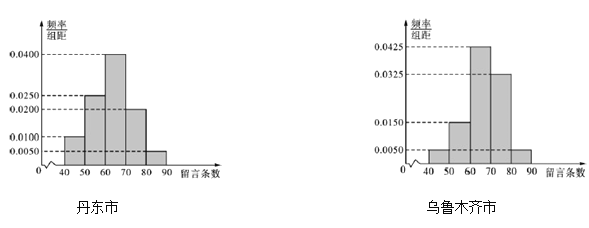
(1)求丹东市网友的平均留言条数(保留整数);
(2)为了进一步开展调查,从样本中留言条数超过80条的网友中随机抽取2人,求至少抽到一名乌鲁木齐市网友的概率;
(3)规定“留言条数”不少于70条为“强烈关注”.
①请你根据已知条件完成下列2×2的列联表:
强烈关注 | 非强烈关注 | 合计 | |
丹东市 | |||
乌鲁木齐市 | |||
合计 |
②判断是否有90%的把握认为“强烈关注”与网友所在的地区有关?
附:临界值表及参考公式:
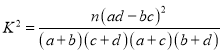 ,
,![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |