题目内容
【题目】在平面直角坐标系中,已知点![]() ,直线
,直线![]() ,动直线
,动直线![]() 垂直
垂直![]() 于点
于点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)以曲线![]() 上的点
上的点![]() 为切点做曲线
为切点做曲线![]() 的切线
的切线![]() ,设
,设![]() 分别与
分别与![]() 、
、![]() 轴交于
轴交于![]() 两点,且
两点,且![]() 恰与以定点
恰与以定点![]() 为圆心的圆相切.当圆
为圆心的圆相切.当圆![]() 的面积最小时,求
的面积最小时,求![]() 与
与![]() 面积的比.
面积的比.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】分析:(I)由![]() ,根据抛物线的定义,点
,根据抛物线的定义,点![]() 的轨迹是以
的轨迹是以![]() 为准线,
为准线,![]() 为焦点的抛物线,即可求得抛物线方程;(II)求直线
为焦点的抛物线,即可求得抛物线方程;(II)求直线![]() 的斜率,解法一,联立直线
的斜率,解法一,联立直线![]() 的方程与抛物线的方程,根据
的方程与抛物线的方程,根据![]() ,即可求得直线
,即可求得直线![]() 的斜率;解法二,当
的斜率;解法二,当![]() 时,
时,![]() ,求导,即可求得切线斜率,然后利用点斜式方程即可求得切线方程,取得
,求导,即可求得切线斜率,然后利用点斜式方程即可求得切线方程,取得![]() 和
和![]() 点坐标,利用点到直线的距离公式,根据基本不等式的性质,当
点坐标,利用点到直线的距离公式,根据基本不等式的性质,当![]() 时,满足题意的圆
时,满足题意的圆![]() 的面积最小,求得
的面积最小,求得![]() 和
和![]() 点坐标,利用三角形的面积公式即可求得△
点坐标,利用三角形的面积公式即可求得△![]() 与△
与△![]() 面积的比.
面积的比.
详解:(Ⅰ)由题意得![]() ,
,
![]() 点
点![]() 到直线
到直线![]() 的距离等于它到定点
的距离等于它到定点![]() 的距离,
的距离,
![]() 点
点![]() 的轨迹是以
的轨迹是以![]() 为准线,
为准线,![]() 为焦点的抛物线,
为焦点的抛物线,
![]() 点
点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]()
(Ⅱ)解法一:由题意知切线![]() 的斜率必然存在,设为
的斜率必然存在,设为![]() ,则
,则![]() .
.
由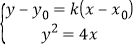 ,得
,得![]() ,即
,即![]() ,由
,由![]() ,得到
,得到![]() .
.
∴![]() ,
,
解法二:由![]() ,当
,当![]() 时,
时,![]() .
.
![]()
![]() 以
以![]() 为切点的切线
为切点的切线![]() 的斜率为
的斜率为![]()
![]() 以
以![]() 为切点的切线为
为切点的切线为![]() ,即
,即![]() ,整理
,整理![]() .
.
令![]() 则
则![]() .
.
![]()
令![]() 则
则![]() .
.
![]()
点![]() 到切线
到切线![]() 的距离
的距离![]() (当且仅当
(当且仅当![]() 时,取等号).
时,取等号).
∴ 当![]() 时,满足题意的圆
时,满足题意的圆![]() 的面积最小.
的面积最小.
∴![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
![]() △
△![]() 与△
与△![]() 面积之比为
面积之比为![]() .
.

【题目】下面给出了2010年亚洲某些国家的国民平均寿命![]() 单位:岁
单位:岁![]() .
.
国家 | 平均寿命 | 国家 | 平均寿命 | 国家 | 平均寿命 |
阿曼 |
| 阿富汗 | 59 | 巴基斯坦 |
|
巴林 | | 阿联酋 |
| 马来西亚 |
|
朝鲜 |
| 东帝汶 |
| 孟加拉国 |
|
韩国 |
| 柬埔寨 |
| 塞浦路斯 |
|
老挝 |
| 卡塔尔 |
| 沙特阿拉伯 |
|
蒙古 |
| 科威特 | | 哈萨克斯坦 |
|
缅甸 |
| 菲律宾 |
| 印度尼西亚 |
|
日本 |
| 黎巴嫩 |
| 土库曼斯坦 | 65 |
泰国 |
| 尼泊尔 | 68 | 吉尔吉斯斯坦 |
|
约旦 |
| 土耳其 |
| 乌兹别克斯坦 |
|
越南 | 75 | 伊拉克 |
| 也门 |
|
中国 |
| 以色列 |
| 文莱 |
|
伊朗 | 74 | 新加坡 |
| 叙利亚 |
|
印度 |
|
![]() 根据这40个国家的样本数据,得到如图所示的频率分布直方图,其中样本数据的分组区间为:
根据这40个国家的样本数据,得到如图所示的频率分布直方图,其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 请根据上述所提供的数据,求出频率分布直方图中的a,b;
请根据上述所提供的数据,求出频率分布直方图中的a,b;
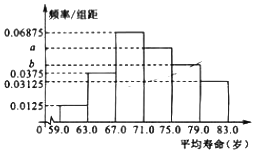
![]() 请根据统计思想,利用
请根据统计思想,利用![]() 中的频率分布直方图估计亚洲人民的平均寿命及国民寿命的中位数
中的频率分布直方图估计亚洲人民的平均寿命及国民寿命的中位数![]() 保留一位小数
保留一位小数![]() .
.