题目内容
【题目】已知点F为抛物线E:x2=4y的焦点,直线l为准线,C为抛物线上的一点(C在第一象限),以点C为圆心,|CF|为半径的圆与y轴交于D,F两点,且△CDF为正三角形. 
(Ⅰ)求圆C的方程;
(Ⅱ)设P为l上任意一点,过P作抛物线x2=4y的切线,切点为A,B,判断直线AB与圆C的位置关系.
【答案】解:(I)由已知F(0,1),设圆C的半径为r, 因为△CDF为正三角形,C( ![]() r,|r﹣1|),
r,|r﹣1|),
因为点C在抛物线x2=4y上,
得 ![]() r2=4r﹣4 即3r2﹣16r+16=0,
r2=4r﹣4 即3r2﹣16r+16=0,
解得r=4或r= ![]()
所以圆C的方程为C1:(x﹣2 ![]() )2+(y﹣3)2=16,
)2+(y﹣3)2=16,
或C2:(x﹣ ![]() )2+(y﹣
)2+(y﹣ ![]() )2=
)2= ![]()
(II)(方法一)
因为准线l为y=﹣1,设P(t,﹣1),A(x1 , y1),B(x2 , y2),
因为y= ![]() ,所以y′=
,所以y′= ![]() ,
,
A(x1 , y1)为切点的切线方程为:y﹣y1= ![]() (x﹣x1),y1=
(x﹣x1),y1= ![]() ,即y=
,即y= ![]() x﹣y1 ,
x﹣y1 ,
因为切线过P(t,﹣1),得﹣1= ![]() t﹣y1 , ①
t﹣y1 , ①
同理可得﹣1= ![]() t﹣y2 , ②
t﹣y2 , ②
所以直线AB方程为﹣1= ![]() xt﹣y,即tx﹣2y+2=0,
xt﹣y,即tx﹣2y+2=0,
圆心C1(2 ![]() ,3),r1=4,C1到直线距离d1=
,3),r1=4,C1到直线距离d1= 
可得d12﹣16= ![]() ≤0
≤0
所以t=﹣2 ![]() 时,d1=4,直线AB与圆C1相切.
时,d1=4,直线AB与圆C1相切.
t≠﹣2 ![]() 时,d1<4直线AB与圆C1相交.
时,d1<4直线AB与圆C1相交.
所以直线AB与圆C2相交或相切.
同理可证,直线AB与圆C2相交或相切.
所以直线AB与圆C1 , C2相交或相切.
(注:因为直线AB过定点f(0,1),且斜率 ![]() ∈R
∈R
因为F(0,1)在圆C1 , C2相上,所以直线AB与圆C1 , C
(方法二)设设P(t,﹣1),A(x1 , y1),B(x2 , y2),
直线AB的方程为y=kx+b,代入抛物线E的方程得x2﹣4kx﹣4b=0 所以x1+x2=4k,x1x2=﹣4b,
因为y= ![]() ,所以y′=
,所以y′= ![]() ,
,
A(x1 , y1)为切点的切线方程为:y﹣y1= ![]() (x﹣x1),y1=
(x﹣x1),y1= ![]() ,即y=
,即y= ![]() x﹣
x﹣ ![]() ,①
,①
B(x2 , y2)为切点的切线方程为y= ![]() x﹣
x﹣ ![]() ②
②
联立①②得 
所以 ![]() 所以
所以 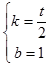 ,
,
所以直线AB方程为y= ![]() xt+1,
xt+1,
以下与(方法一)相同
【解析】(Ⅰ)求出点C的坐标,再代入到抛物线的解析式中求出半径,问题得以解决;(Ⅱ)设P(t,﹣1),A(x1 , y1),B(x2 , y2),根据导数和几何意义,求出A,B为切点的切线方程,即可得到直线AB的方程,再利用点到直线的距离,和半径的关系判断直线和圆的位置关系.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案