题目内容
(本小题满分12分)
设函数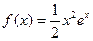 .
.
⑴求函数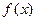 的单调区间;
的单调区间;
⑵若当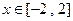 时,不等式
时,不等式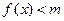 恒成立,求实数
恒成立,求实数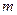 的取值范围.
的取值范围.
设函数
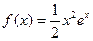 .
.⑴求函数
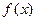 的单调区间;
的单调区间;⑵若当
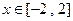 时,不等式
时,不等式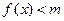 恒成立,求实数
恒成立,求实数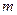 的取值范围.
的取值范围.⑴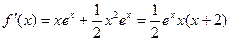 , ………………2分
, ………………2分
令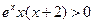 ,得
,得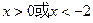 ,
,
∴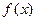 的增区间为
的增区间为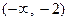 和
和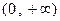 , …………………4分
, …………………4分
令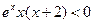 ,得
,得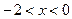 ,
,
∴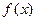 的减区间为
的减区间为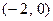 . ……………………6分
. ……………………6分
⑵因为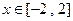 ,令
,令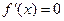 ,得
,得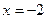 ,或
,或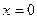 ,
,
又由⑴知,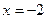 ,
,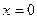 分别为
分别为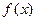 的极小值点和极大值点, ………8分
的极小值点和极大值点, ………8分
∵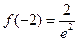 ,
,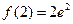 ,
,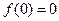 ,
,
∴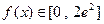 , ……………………………11分
, ……………………………11分
∴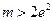 . ……………………………12分
. ……………………………12分
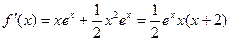 , ………………2分
, ………………2分令
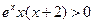 ,得
,得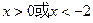 ,
,∴
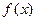 的增区间为
的增区间为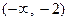 和
和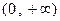 , …………………4分
, …………………4分令
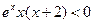 ,得
,得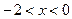 ,
,∴
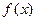 的减区间为
的减区间为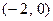 . ……………………6分
. ……………………6分⑵因为
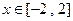 ,令
,令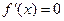 ,得
,得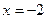 ,或
,或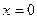 ,
,又由⑴知,
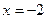 ,
,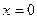 分别为
分别为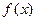 的极小值点和极大值点, ………8分
的极小值点和极大值点, ………8分∵
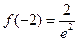 ,
,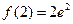 ,
,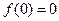 ,
,∴
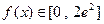 , ……………………………11分
, ……………………………11分∴
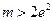 . ……………………………12分
. ……………………………12分略

练习册系列答案
相关题目
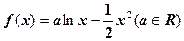 。(1)讨论函数
。(1)讨论函数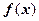 的单调性;(2)当
的单调性;(2)当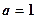 时,设
时,设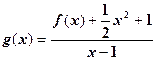 ,若
,若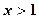 时,
时,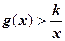 恒成立。求整数
恒成立。求整数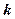 的最大值。
的最大值。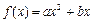 的图像过
的图像过 点
点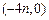 ,且
,且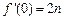 ,
,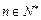 .
.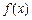 的解析式;
的解析式; 满足
满足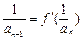 ,且
,且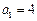 ,求数列
,求数列 ,
,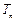 为数列
为数列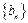 的前
的前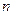 项和.求证:
项和.求证: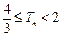 .
.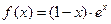 的单调递增区间是
的单调递增区间是  .
. 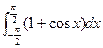 =__________________________.
=__________________________.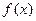 满足
满足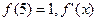 为
为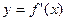 的图像如图所示,若两个正整数
的图像如图所示,若两个正整数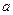 ,
,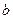 满足
满足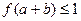 ,集合
,集合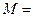
 若从
若从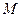 中任取两个点,则两点都不在直线
中任取两个点,则两点都不在直线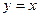 上的概率为 。
上的概率为 。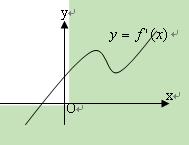
 的图象与直线
的图象与直线 相切, 则
相切, 则



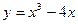 在点
在点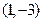 处的切线倾斜角为__________。
处的切线倾斜角为__________。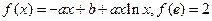 (e=2.71828…是自然对数的底数).
(e=2.71828…是自然对数的底数).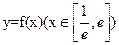 都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.