题目内容
(本小题满分12分)
已知函数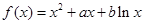 (
(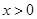 ,实数
,实数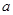 ,
,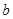 为常数).
为常数).
(Ⅰ)若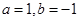 ,求
,求 在
在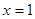 处的切线方程;
处的切线方程;
(Ⅱ)若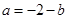 ,讨论函数
,讨论函数 的单调性.
的单调性.
已知函数
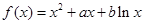 (
(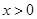 ,实数
,实数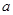 ,
,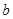 为常数).
为常数).(Ⅰ)若
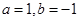 ,求
,求 在
在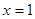 处的切线方程;
处的切线方程;(Ⅱ)若
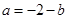 ,讨论函数
,讨论函数 的单调性.
的单调性.(Ⅰ)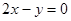 ;
;
(Ⅱ)当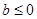 时,函数
时,函数 的单调递减区间为
的单调递减区间为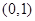 ,单调递增区间为
,单调递增区间为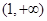 ;当
;当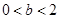 时,函数
时,函数 的单调递增区间为
的单调递增区间为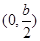 ,
,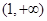 ,单调递减区间为
,单调递减区间为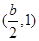 ;当
;当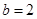 时,函数
时,函数 的单调递增区间为
的单调递增区间为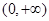 ;当
;当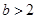 时,函数
时,函数 的单调递增区间为
的单调递增区间为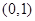 ,
,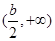 ,单调递减区间为
,单调递减区间为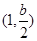 .
.
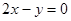 ;
;(Ⅱ)当
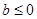 时,函数
时,函数 的单调递减区间为
的单调递减区间为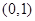 ,单调递增区间为
,单调递增区间为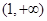 ;当
;当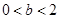 时,函数
时,函数 的单调递增区间为
的单调递增区间为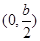 ,
,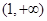 ,单调递减区间为
,单调递减区间为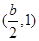 ;当
;当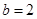 时,函数
时,函数 的单调递增区间为
的单调递增区间为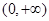 ;当
;当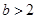 时,函数
时,函数 的单调递增区间为
的单调递增区间为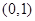 ,
,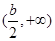 ,单调递减区间为
,单调递减区间为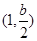 .
.(1)把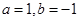 ,代入
,代入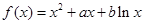 ,可求出
,可求出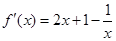 ,当
,当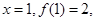
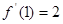 ,由点斜式方程写出曲线的切线方程,再化为一般式;(2)把
,由点斜式方程写出曲线的切线方程,再化为一般式;(2)把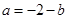 代入得
代入得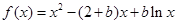 ,
,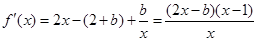 ,注意定义域,令
,注意定义域,令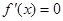 ,得
,得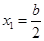 ,
,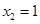 .需讨论
.需讨论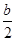 与0和1的大小得
与0和1的大小得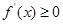 或
或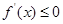 的
的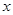 的范围,就是原函数的增区间或减区间.
的范围,就是原函数的增区间或减区间.
(Ⅰ)因为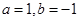 ,所以函数
,所以函数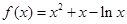 ,
,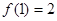
又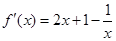 ,
,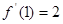 ………………………………………………2分
………………………………………………2分
所以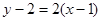
即 在
在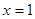 处的切线方程为
处的切线方程为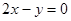 …………………………………5分
…………………………………5分
(Ⅱ)因为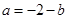 ,所以
,所以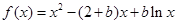 ,则
,则
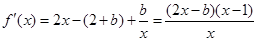
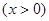
令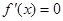 ,得
,得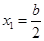 ,
,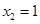 .……………………………………………7分
.……………………………………………7分
(1)当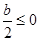 ,即
,即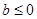 时,函数
时,函数 的单调递减区间为
的单调递减区间为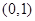 ,
,
单调递增区间为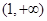 ;…………………………………………8分
;…………………………………………8分
(2)当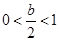 ,即
,即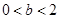 时,
时,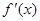 ,
, 的变化情况如下表:
的变化情况如下表:
所以,函数 的单调递增区间为
的单调递增区间为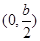 ,
,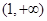 ,
,
单调递减区间为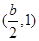 ;…………………………9分
;…………………………9分
(3)当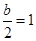 ,即
,即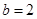 时,函数
时,函数 的单调递增区间为
的单调递增区间为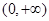 ;………10分
;………10分
(4)当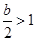 ,即
,即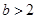 时,
时,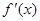 ,
, 的变化情况如下表:
的变化情况如下表:
所以函数 的单调递增区间为
的单调递增区间为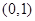 ,
,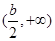 ,单调递减区间为
,单调递减区间为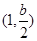 ;……………………………………11分
;……………………………………11分
综上,当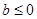 时,函数
时,函数 的单调递减区间为
的单调递减区间为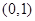 ,单调递增区间为
,单调递增区间为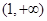 ;当
;当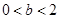 时,函数
时,函数 的单调递增区间为
的单调递增区间为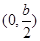 ,
,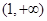 ,单调递减区间为
,单调递减区间为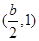 ;当
;当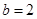 时,函数
时,函数 的单调递增区间为
的单调递增区间为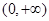 ;当
;当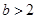 时,函数
时,函数 的单调递增区间为
的单调递增区间为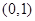 ,
,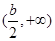 ,单调递减区间为
,单调递减区间为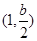 .…………………………12分
.…………………………12分
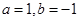 ,代入
,代入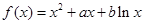 ,可求出
,可求出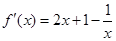 ,当
,当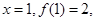
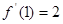 ,由点斜式方程写出曲线的切线方程,再化为一般式;(2)把
,由点斜式方程写出曲线的切线方程,再化为一般式;(2)把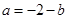 代入得
代入得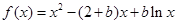 ,
,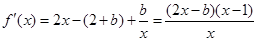 ,注意定义域,令
,注意定义域,令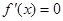 ,得
,得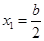 ,
,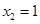 .需讨论
.需讨论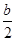 与0和1的大小得
与0和1的大小得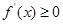 或
或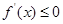 的
的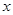 的范围,就是原函数的增区间或减区间.
的范围,就是原函数的增区间或减区间.(Ⅰ)因为
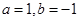 ,所以函数
,所以函数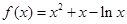 ,
,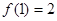
又
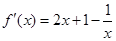 ,
,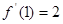 ………………………………………………2分
………………………………………………2分所以
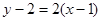
即
 在
在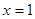 处的切线方程为
处的切线方程为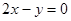 …………………………………5分
…………………………………5分(Ⅱ)因为
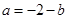 ,所以
,所以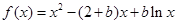 ,则
,则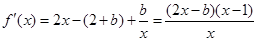
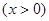
令
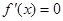 ,得
,得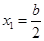 ,
,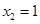 .……………………………………………7分
.……………………………………………7分(1)当
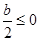 ,即
,即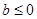 时,函数
时,函数 的单调递减区间为
的单调递减区间为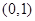 ,
,单调递增区间为
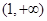 ;…………………………………………8分
;…………………………………………8分(2)当
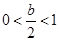 ,即
,即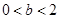 时,
时,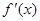 ,
, 的变化情况如下表:
的变化情况如下表: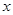 | 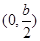 | 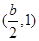 | 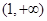 |
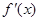 | 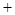 | 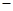 | 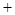 |
 |  |  |  |
 的单调递增区间为
的单调递增区间为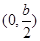 ,
,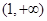 ,
,单调递减区间为
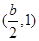 ;…………………………9分
;…………………………9分(3)当
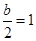 ,即
,即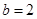 时,函数
时,函数 的单调递增区间为
的单调递增区间为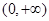 ;………10分
;………10分(4)当
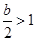 ,即
,即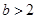 时,
时,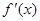 ,
, 的变化情况如下表:
的变化情况如下表: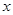 | 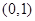 | 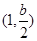 | 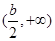 |
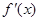 | 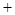 |  | 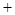 |
 |  |  |  |
所以函数
 的单调递增区间为
的单调递增区间为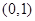 ,
,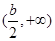 ,单调递减区间为
,单调递减区间为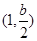 ;……………………………………11分
;……………………………………11分综上,当
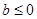 时,函数
时,函数 的单调递减区间为
的单调递减区间为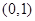 ,单调递增区间为
,单调递增区间为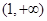 ;当
;当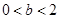 时,函数
时,函数 的单调递增区间为
的单调递增区间为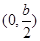 ,
,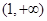 ,单调递减区间为
,单调递减区间为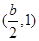 ;当
;当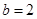 时,函数
时,函数 的单调递增区间为
的单调递增区间为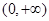 ;当
;当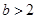 时,函数
时,函数 的单调递增区间为
的单调递增区间为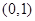 ,
,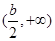 ,单调递减区间为
,单调递减区间为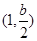 .…………………………12分
.…………………………12分
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 ,其中
,其中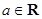 .
.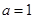 时,求曲线
时,求曲线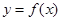 在原点处的切线方程;
在原点处的切线方程;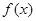 的单调区间.
的单调区间.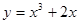 相切的直线方程为_______ __ ;
相切的直线方程为_______ __ ; 的图象经过点
的图象经过点 ,则它在
,则它在 点处的切线方程为
点处的切线方程为



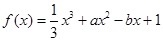 (
(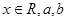 为实数)有极值,且在
为实数)有极值,且在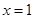 处的切线与直线
处的切线与直线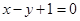 平行.
平行.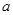 的取值范围;
的取值范围;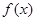 的极小值为1,若存在,求出实数
的极小值为1,若存在,求出实数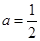 ,
,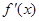 ,令
,令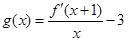
 相同的方向移动,那么从位置
相同的方向移动,那么从位置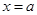 到
到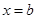 变力所做的功
变力所做的功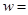 .
. 与
与 围成的区域面积为
围成的区域面积为 




 分别满足
分别满足 且
且 = 。
= 。 :
: 和点
和点 ,则过点
,则过点 且与曲线
且与曲线