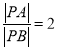题目内容
【题目】已知抛物线![]() :
:![]() ,直线
,直线![]() 截抛物线
截抛物线![]() 所得弦长为
所得弦长为![]() .
.
(1)求![]() 的值;
的值;
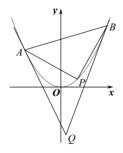
(2)若直角三角形![]() 的三个顶点在抛物线
的三个顶点在抛物线![]() 上,且直角顶点
上,且直角顶点![]() 的横坐标为1,过点
的横坐标为1,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线,两切线相交于点
的切线,两切线相交于点![]() .
.
①若直线![]() 经过点
经过点![]() ,求点
,求点![]() 的纵坐标;
的纵坐标;
②求![]() 的最大值及此时点
的最大值及此时点![]() 的坐标.
的坐标.
【答案】(1)![]() (2)①-3.②最大值见解析,
(2)①-3.②最大值见解析,![]()
【解析】
(1)联立![]() ,求出交点,利用两点距离公式列方程求解即可;
,求出交点,利用两点距离公式列方程求解即可;
(2)①设点![]() ,
,![]() ,
,![]() ,切线
,切线![]() :
:![]() ,
,![]() :
:![]() ,化归为二次方程的根的问题,可得直线
,化归为二次方程的根的问题,可得直线![]() 的方程,代入点
的方程,代入点![]() ,即可得点
,即可得点![]() 的纵坐标;②由题设知
的纵坐标;②由题设知![]() ,即
,即![]() ,利用面积公式表示出
,利用面积公式表示出![]() ,利用函数的性质求其最值.
,利用函数的性质求其最值.
解:(1)![]() ,解得两交点为
,解得两交点为![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
(2)①设点![]() ,
,![]() ,
,![]() .切线
.切线![]() :
:![]() ,
,![]() :
:![]() ,
,
由题设知![]() ,
,![]() ,
,
即![]() ,
,![]() 是方程
是方程![]() 的两根,于是
的两根,于是![]() ,
,![]() .
.
故直线![]() :
:![]() .又因为直线
.又因为直线![]() 经过点
经过点![]() ,
,
所以![]() ,即点
,即点![]() 的纵坐标为-3;
的纵坐标为-3;
②由题设知![]() ,即
,即![]() .
.
则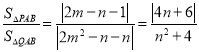 ,
,
若![]() ,令
,令![]() ,
,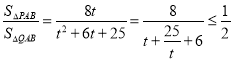 ,
,
若![]() ,令
,令![]() ,
,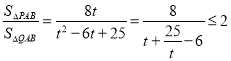 ,
,
当且仅当![]() ,
,![]() 时,等号成立,此时点
时,等号成立,此时点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目