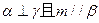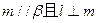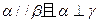题目内容
(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是正方形,PA⊥平面ABCD,且PA=AB=2,E、F分别为AB、PC的中点。
(1)求异面直线PA与BF所成角的正切值。
(2) 求证:EF⊥平面PCD。
求证:EF⊥平面PCD。
如图,在四棱锥P—ABCD中,底面ABCD是正方形,PA⊥平面ABCD,且PA=AB=2,E、F分别为AB、PC的中点。
(1)求异面直线PA与BF所成角的正切值。
(2)
 求证:EF⊥平面PCD。
求证:EF⊥平面PCD。解:(1)如图,连结AC
过点F作FO⊥AC,
∴面PAC⊥面ABCD
∵PA⊥平面ABCD,
∴平面PAC⊥AC,垂足为O,
连结BO,则FO⊥平面ABCD,且FO//PA。
∴∠BFO为异面直线PA与BF所成的角………………4分
在Rt△BOF中,OF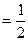 PA=1,
PA=1,
OB=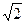 ,则tanBFO=
,则tanBFO= ………………6分
………………6分
(2)连结OE、CE、PE。
∵E是AB的中点,
∴OE⊥AB
又FO⊥平面ABCD,
∴EF⊥AB。
∵AB//CD
∴EF⊥CD
在Rt△PAE和Rt△CBE中,PA=CB,AE=BE,
∴Rt△PAE≌Rt△CBE,
∴PE=CE…………………………10分
∴又F为PC的中点,
 ∴EF⊥PC。
∴EF⊥PC。
故EF⊥平面PCD。……………………12分
过点F作FO⊥AC,
∴面PAC⊥面ABCD
∵PA⊥平面ABCD,
∴平面PAC⊥AC,垂足为O,
连结BO,则FO⊥平面ABCD,且FO//PA。
∴∠BFO为异面直线PA与BF所成的角………………4分
在Rt△BOF中,OF
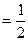 PA=1,
PA=1,OB=
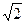 ,则tanBFO=
,则tanBFO= ………………6分
………………6分(2)连结OE、CE、PE。
∵E是AB的中点,
∴OE⊥AB
又FO⊥平面ABCD,
∴EF⊥AB。
∵AB//CD
∴EF⊥CD
在Rt△PAE和Rt△CBE中,PA=CB,AE=BE,
∴Rt△PAE≌Rt△CBE,
∴PE=CE…………………………10分
∴又F为PC的中点,
 ∴EF⊥PC。
∴EF⊥PC。故EF⊥平面PCD。……………………12分
略

练习册系列答案
相关题目
 中,底面
中,底面 是直角梯形,
是直角梯形,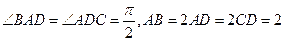
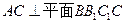
 上是否存一点
上是否存一点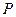 ,使得
,使得 与平面
与平面 与平面
与平面 都平行?证明你的结论.
都平行?证明你的结论.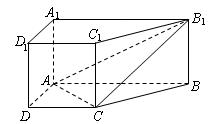
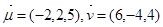 分别是平面
分别是平面 的法向量,则平面
的法向量,则平面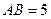 ,AA1=3,点D是AB的中点.
,AA1=3,点D是AB的中点.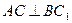
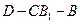 的大小.
的大小.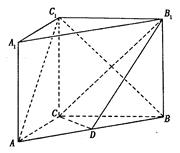
 中,
中, 平面
平面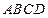 ,
,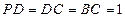 ,
,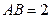 ,
,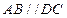 ,
,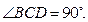
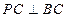 ;
;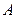 到平面
到平面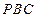 的距离
的距离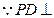 平面
平面 又
又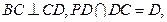
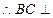 平面
平面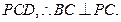 (4分)
(4分)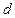 ,
,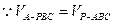 ,
,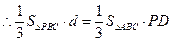 ,
,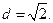 即点
即点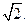 (8分)
(8分) 方形
方形 的边
的边 、
、 的中点,沿SE、SF、EF将它折成一个几何体,使
的中点,沿SE、SF、EF将它折成一个几何体,使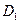 、D、
、D、 重合,记作D,给出下列位
重合,记作D,给出下列位 置关系:
置关系: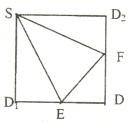
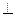 面EFD;②SE
面EFD;②SE 中,直线
中,直线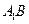 和直线
和直线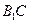 所成的角的大小为( ).
所成的角的大小为( ).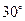
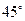


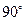
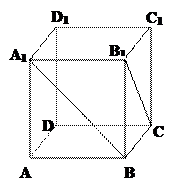
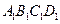 中E是AB的中点,O是侧面
中E是AB的中点,O是侧面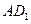 的中心.
的中心.








 ,那么必有( )
,那么必有( )