题目内容
【题目】已知![]() .
.
(1)若关于![]() 的方程
的方程![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的值;
的值;
(2)证明:当![]() 时,
时, ![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)令![]() ,讨论
,讨论![]() 的取值,只需
的取值,只需![]() 即可;
即可;
(2)由(1)知![]() 时,
时, ![]() ,即
,即![]() 恒成立,令
恒成立,令![]() ,即
,即![]() ,一次赋值
,一次赋值![]() ,再累加得
,再累加得![]() ,再取对数即可.
,再取对数即可.
试题解析:
(1)令![]() ,
,
若![]() ,与已知矛盾,
,与已知矛盾,
若![]() ,则
,则![]() ,显然不满足在
,显然不满足在![]() 上
上![]() 恒成立,
恒成立,
若![]() ,对
,对![]() 求导可得
求导可得![]() ,
,
由![]() 解得
解得![]() ,由
,由![]() 解得
解得![]() ,
,
∴![]() 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
∴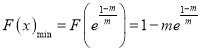 , ∴要使
, ∴要使![]() 恒成立,则须使
恒成立,则须使![]() 成立,
成立,
即![]() 恒成立,两边取对数得,
恒成立,两边取对数得, ![]() ,整理得
,整理得![]() ,即须此式成立,
,即须此式成立,
令![]() ,则
,则![]() ,显然当
,显然当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,于是函数
,于是函数![]() 的
的![]() 上单调递减,在
上单调递减,在![]() 单调递增,
单调递增,
∴![]() ,即当且仅当
,即当且仅当![]() 时,
时, ![]() 恒成立,
恒成立,
∴![]() 满足条件,综上所述,
满足条件,综上所述, ![]() .
.
(2)由(1)知![]() 时,
时, ![]() ,即
,即![]() 恒成立,
恒成立,
令![]() ,即
,即![]() ,
,
即![]() ,同理,
,同理, ![]() ,
,
![]() ,
,
![]() ,
,
将上式左右相加得: ![]() ,
,
即![]() ,即
,即![]() .
.

练习册系列答案
相关题目



