题目内容
【题目】已知椭圆![]() (
(![]() )的焦距为2,椭圆
)的焦距为2,椭圆![]() 的左右焦点分别为
的左右焦点分别为![]()
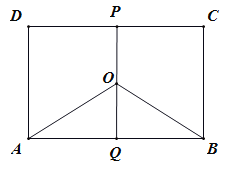
![]() ,过右焦点
,过右焦点![]() 作
作![]() 轴的垂线交椭圆于
轴的垂线交椭圆于![]()
![]() 两点,
两点,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 作直线交椭圆于
作直线交椭圆于![]()
![]() 两点,若△
两点,若△![]() 的内切圆的面积为
的内切圆的面积为![]() ,求△
,求△![]() 的面积;
的面积;
(3)已知![]() ,
,![]() 为圆上一点(
为圆上一点(![]() 在
在![]() 轴右侧),过
轴右侧),过![]() 作圆的切线交椭圆
作圆的切线交椭圆![]() 于
于![]()
![]() 两点,试问△
两点,试问△![]() 的周长是否为一定值?若是,求出该定值,若不是,请说明理由.
的周长是否为一定值?若是,求出该定值,若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)是,
;(3)是,![]() .
.
【解析】
(1)由题意结合椭圆的性质可得![]() ,再由点
,再由点![]() 即可求得
即可求得![]() 、
、![]() ,即可得解;
,即可得解;
(2)由题意结合椭圆的性质可得△![]() 的周长
的周长![]() ,再由
,再由![]() (
(![]() 为内切圆半径)即可得解;
为内切圆半径)即可得解;
(3)按照![]() 斜率是否存在讨论,当直线
斜率是否存在讨论,当直线![]() 斜率存在时,设
斜率存在时,设![]() ,
,![]() ,由两点之间距离公式、椭圆性质可得焦半径
,由两点之间距离公式、椭圆性质可得焦半径![]() 、
、![]() ,联立方程结合韦达定理、弦长公式可得
,联立方程结合韦达定理、弦长公式可得![]() ,再由直线
,再由直线![]() 与圆相切可得
与圆相切可得![]() ,代入运算即可得解.
,代入运算即可得解.
(1)由椭圆焦距为2可得![]() ,
,![]() ,
,
又过右焦点![]() 作
作![]() 轴的垂线交椭圆于
轴的垂线交椭圆于![]() 、
、![]() 两点,
两点,![]() ,
,
不妨设点![]() ,则
,则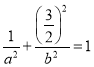 ,解得
,解得![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ;
;
(2)由题意△![]() 的周长
的周长![]() ,
,
又△![]() 的内切圆的面积为
的内切圆的面积为![]() ,所以△
,所以△![]() 的内切圆的半径为
的内切圆的半径为![]() ,
,
所以△![]() 的面积
的面积![]() ;
;
(3)由题意![]() ,圆心为
,圆心为![]() ,半径为
,半径为![]() ,
,
若![]() 斜率不存在时,不妨设点
斜率不存在时,不妨设点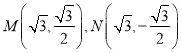 ,
,
此时△![]() 的周长
的周长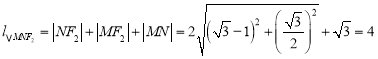 ;
;
当直线![]() 斜率存在时,设
斜率存在时,设![]() ,
,![]() ,
,
则![]() 即
即![]() ,
,
则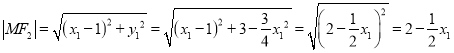 ,
,
同理,![]() ,
,
由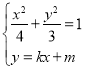 消去y得
消去y得![]() ,
,![]() ,
,
则![]() ,
,
由直线![]() 与
与![]() 相切可得
相切可得![]() ,即
,即![]() ,
,
所以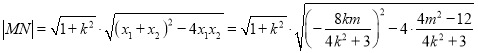
![]() ,
,
因为![]() 在
在![]() 轴右侧,所以
轴右侧,所以![]() ,
,
所以![]()
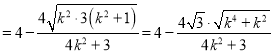 ,
,
所以△![]() 的周长
的周长![]()
![]() ;
;
综上,△![]() 的周长为一定值,且周长
的周长为一定值,且周长![]() .
.

【题目】中国人民大学发布的《中国大学生创业报告》显示,在国家“双创”政策的引导下,随着社会各方对于大学生创业实践的支持力度不断加强,大学生创业意向高涨,近九成的在校大学生曾考虑过创业,近两成的学生有强烈的创业意向. 数据充分表明,大学生正以饱满的热情投身到创新创业的大潮之中,大学生创业实践正呈现出生机勃勃的态势。小张大学毕业后从2008年年初开始创业,下表是2019年春节他将自己从2008—2018年的净利润按年度给出的一个总的统计表(为方便运算,数据作了适当的处理,单位:万元).
年度 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
利润 | 6 | 7 | 8 | 9 | 10 | 10 | 11 | 12 | 13 | 13 | 14 |
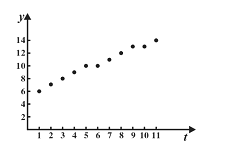
(Ⅰ)散点图如图所示,根据散点图指出年利润![]() (单位:万元)和年份序号
(单位:万元)和年份序号![]() 之间是否具有线性关系?并用相关系数说明用线性回归模型描述年净利润
之间是否具有线性关系?并用相关系数说明用线性回归模型描述年净利润![]() 与年份序号
与年份序号![]() 之间关系的效果;
之间关系的效果;
(Ⅱ)试用线性回归模型描述年净利润![]() 与年份序号
与年份序号![]() 之间的关系:求出年净利润
之间的关系:求出年净利润![]() 关于年份序号
关于年份序号![]() 的回归方程(系数精确到0.1),并帮小张估计他2019年可能赚到的净利润.
的回归方程(系数精确到0.1),并帮小张估计他2019年可能赚到的净利润.
附注:参考数据![]() .
.
参考公式: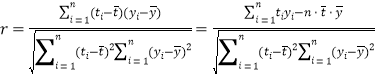 .
.![]() 且
且![]() 越大拟合效果越好.回归方程
越大拟合效果越好.回归方程![]() 斜率的最小二乘法估计公式为:
斜率的最小二乘法估计公式为: .
.