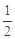题目内容
已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<
),y=f(x)的部分图象如图,则f(
)=______.

| π |
| 2 |
| π |
| 24 |

由题意可知T=
,所以ω=2,
函数的解析式为:f(x)=Atan(ωx+φ),因为函数过(
,0)所以0=Atan(
+φ)所以φ=
,
图象经过(0,1),所以,1=Atan
,所以A=1,所以f(x)=tan(2x+
)则f(
)=tan(
+
)=
故答案为:
| π |
| 2 |
函数的解析式为:f(x)=Atan(ωx+φ),因为函数过(
| 3π |
| 8 |
| 3π |
| 4 |
| π |
| 4 |
图象经过(0,1),所以,1=Atan
| π |
| 4 |
| π |
| 4 |
| π |
| 24 |
| π |
| 12 |
| π |
| 4 |
| 3 |
故答案为:
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
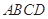 中,
中,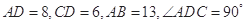 ,且
,且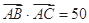 .
.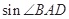 的值;(2)设
的值;(2)设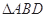 的面积为
的面积为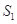 ,四边形
,四边形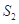 ,求
,求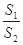 的值.
的值.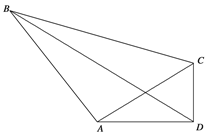



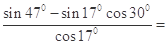 ( ).
( ).