题目内容
如图,在四边形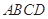 中,
中,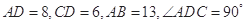 ,且
,且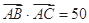 .
.
(1)求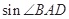 的值;(2)设
的值;(2)设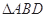 的面积为
的面积为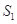 ,四边形
,四边形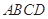 的面积为
的面积为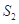 ,求
,求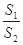 的值.
的值.
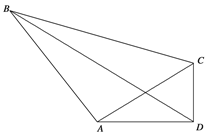
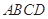 中,
中,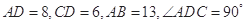 ,且
,且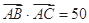 .
.(1)求
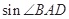 的值;(2)设
的值;(2)设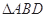 的面积为
的面积为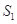 ,四边形
,四边形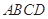 的面积为
的面积为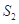 ,求
,求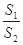 的值.
的值.
(1)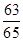 ,(2)
,(2)  .
.
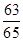 ,(2)
,(2)  .
.试题分析:(1)由于
 ,而
,而 的余弦值可通过cos∠BAC=
的余弦值可通过cos∠BAC= 求得,进而可求得
求得,进而可求得 的正弦值,对于
的正弦值,对于 的正余弦值可通过
的正余弦值可通过 边角关系求得,再用两角和的正弦公式求得
边角关系求得,再用两角和的正弦公式求得 的正弦值;(2)利用两边一夹角的三角形面积公式可求得
的正弦值;(2)利用两边一夹角的三角形面积公式可求得 面积,则
面积,则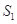 与
与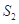 易求得.
易求得.试题解析:(1)在Rt△ADC中,AD=8,CD=6,
则AC=10,cos∠CAD=
 ,sin∠CAD=
,sin∠CAD=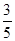 ,
,又∵
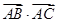 =50,AB=13,
=50,AB=13,∴cos∠BAC=
 =
= ,
,∵0<∠BAC∠180°,
∴sin∠BAC=
 ,
,∴sin∠BAD=sin(∠BAC+∠CAD)=
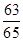 ,
,(2)S1=
 AB·ADsin∠BAD=
AB·ADsin∠BAD= ,
,S△BAC=
 AB·ACsin∠BAC=60,S△ACD=24,
AB·ACsin∠BAC=60,S△ACD=24,则S2=S△ABC+S△ACD=84,
∴
 .
.
练习册系列答案
相关题目

 ,
,
 ;
; 。
。 =
= ,则sin θ+cos θ=________.
,则sin θ+cos θ=________. 是( )
是( ) 的偶函数
的偶函数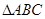 中,内角
中,内角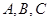 所对的边分别为
所对的边分别为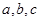 ,且
,且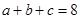
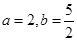 ,求
,求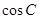 的值;
的值;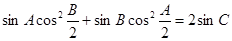 ,且
,且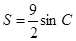 ,求
,求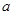 和
和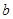 的值.
的值.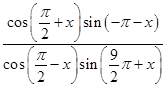 的值为 .
的值为 . 的值为_____.
的值为_____. ,则
,则 =
=