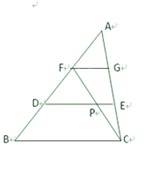
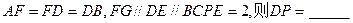题目内容
如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F,
求证:PB2=PE•PF.
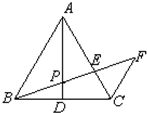
求证:PB2=PE•PF.

连接PC,
∵AB=AC,AD是中线,
∴AD是△ABC的对称轴.
∴PC=PB,∠PCE=∠ABP.
∵CF∥AB,∴∠PFC=∠ABP,
∴∠PCE=∠PFC.
又∠CPE=∠EPC,
∴△EPC∽△CPF.
∴
=
.
∴PC2=PE•PF.
∴PB2=PE•PF.
∵AB=AC,AD是中线,
∴AD是△ABC的对称轴.
∴PC=PB,∠PCE=∠ABP.
∵CF∥AB,∴∠PFC=∠ABP,
∴∠PCE=∠PFC.
又∠CPE=∠EPC,
∴△EPC∽△CPF.
∴
| PC |
| PE |
| PF |
| PC |
∴PC2=PE•PF.
∴PB2=PE•PF.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
 ,则它们的三角形面积比是____________.
,则它们的三角形面积比是____________.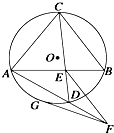

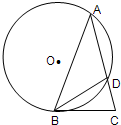

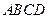 中,
中,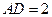 ,
,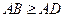 ,
,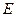 为
为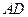 的中点,
的中点,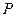 是
是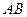 边上一动点.
边上一动点.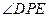 取得最大时,
取得最大时,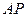 等于
等于