题目内容
【题目】已知椭圆C1: ![]() =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e= ![]() ,且过点(1,
,且过点(1, ![]() ).抛物线C2:x2=﹣2py(p>0)的焦点坐标为(0,﹣
).抛物线C2:x2=﹣2py(p>0)的焦点坐标为(0,﹣ ![]() ).
).
(Ⅰ)求椭圆C1和抛物线C2的方程;
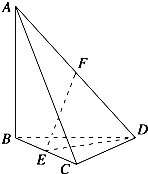
(Ⅱ)若点M是直线l:2x﹣4y+3=0上的动点,过点M作抛物线C2的两条切线,切点分别为A,B,直线AB交椭圆C1于P,Q两点.
(i)求证直线AB过定点,并求出该定点坐标;
(ii)当△OPQ的面积取最大值时,求直线AB的方程.
【答案】解:(I)由于椭圆C1中, ![]() ,
,
则设其方程为 ![]() ,
,
由于点 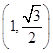 在椭圆上,故代入得λ=1.
在椭圆上,故代入得λ=1.
故椭圆C1的方程为 ![]() .
.
抛物线C2中,
∵抛物线C2:x2=﹣2py(p>0)的焦点坐标为(0,﹣ ![]() ),
),
∴ ![]() ,故p=1,
,故p=1,
从而椭圆C1的方程为 ![]() ,抛物线C2的方程为x2=﹣2y.
,抛物线C2的方程为x2=﹣2y.
(II)(i)证明:设点M(x0 , y0),且满足2x0﹣4y0+3=0,
点A(x1 , y1),B(x2 , y2),则切线MA的斜率为﹣x1 ,
从而MA的方程为y=﹣x1(x﹣x1)+y1 ,
考虑到 ![]() ,则切线MA的方程为x1x+y+y1=0,
,则切线MA的方程为x1x+y+y1=0,
同理切线MB的方程为x2x+y+y2=0,
由于切线MA,MB同过点M,
从而有 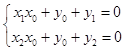 ,
,
由此点A(x1 , y1),B(x2 , y2)在直线x0x+y+y0=0上.
又点M在直线2x﹣4y+3=0上,则2x0﹣4y0+3=0,
故直线AB的方程为(4y0﹣3)x+2y+2y0=0,
即y0(4x+2)+(2y﹣3x)=0,
∴直线AB过定点 ![]() .
.
(ii)解:设P(x3 , y3),Q(x4 , y4),
考虑到直线AB的方程为x0x+y+y0=0,
则联立方程 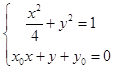 ,
,
消去y并简化得 ![]() ,
,
从而 ![]() ,
, ![]() ,
, ![]() ,
,
从而 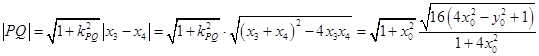 ,
,
点O到PQ的距离 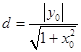 ,
,
从而 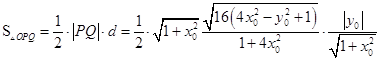
= 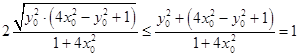 ,
,
当且仅当 ![]() ,即
,即 ![]() ,
,
又由于2x0﹣4y0+3=0,
从而消去x0得 ![]() ,
,
即 ![]() ,解得
,解得 ![]() ,
,
从而 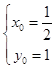 或
或 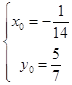 ,
,
∴所求的直线为x+2y+2=0或x﹣14y﹣10=0
【解析】(I)由已知条件,设椭圆方程为 ![]() ,把点
,把点 ![]() 代入能求出椭圆C1的方程.抛物线C2中,由
代入能求出椭圆C1的方程.抛物线C2中,由 ![]() ,能求出抛物线C2的方程.(II)(i)设点M(x0 , y0),且满足2x0﹣4y0+3=0,点A(x1 , y1),B(x2 , y2),由于切线MA,MB同过点M,有
,能求出抛物线C2的方程.(II)(i)设点M(x0 , y0),且满足2x0﹣4y0+3=0,点A(x1 , y1),B(x2 , y2),由于切线MA,MB同过点M,有 ![]() ,由此能证明直线AB过定点
,由此能证明直线AB过定点 ![]() .(ii)设P(x3 , y3),Q(x4 , y4),联立方程
.(ii)设P(x3 , y3),Q(x4 , y4),联立方程 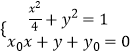 ,得
,得 ![]() ,由此利用根的判别式和韦达定理能求出直线方程.
,由此利用根的判别式和韦达定理能求出直线方程.

 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
[145.5,149.5) | 1 | 0.02 |
[149.5,153.5) | 4 | 0.08 |
[153.5,157.5) | 20 | 0.40 |
[157.5,161.5) | 15 | 0.30 |
[161.5,165.5) | 8 | 0.16 |
[165.5,169.5) | m | n |
合 计 | M | N |

(1)求出表中![]() 所表示的数;
所表示的数;
(2)画出频率分布直方图;