题目内容
18.设Sn为等差数列{an}的前n项和,已知{an}的公差为d,且a1=$\frac{3}{2}$d>0,证明:存在正常数c,使$\sqrt{{S}_{n}+c}+\sqrt{{S}_{n+2}+c}=2\sqrt{{S}_{n+1}+c}$对任意自然数n都成立.分析 先取n=1,确定c=$\frac{1}{2}$d.再证明当c=$\frac{1}{2}$d时,$\sqrt{{S}_{n}+c}+\sqrt{{S}_{n+2}+c}=2\sqrt{{S}_{n+1}+c}$恒成立.
解答 证明:假设存在正常数c使得$\sqrt{{S}_{n}+c}+\sqrt{{S}_{n+2}+c}=2\sqrt{{S}_{n+1}+c}$恒成立.
∵a1=$\frac{3}{2}$d,
∴Sn=$\frac{1}{2}$dn2+dn
令n=1,则有$\sqrt{\frac{3}{2}d+c}$+$\sqrt{\frac{15}{2}d+c}$=2$\sqrt{4d+c}$恒成立两边平方化简得:c=$\frac{1}{2}$d.
以下证明当c=$\frac{1}{2}$d时,$\sqrt{{S}_{n}+c}+\sqrt{{S}_{n+2}+c}=2\sqrt{{S}_{n+1}+c}$恒成立.
$\sqrt{{S}_{n}+c}$+$\sqrt{{S}_{n+2}+c}$-2$\sqrt{{S}_{n+1}+c}$=(n+1)$\sqrt{\frac{d}{2}}$+(n+3)$\sqrt{\frac{d}{2}}$-2(n+2)$\sqrt{\frac{d}{2}}$=0
∴存在正常数c=$\frac{1}{2}$d使$\sqrt{{S}_{n}+c}+\sqrt{{S}_{n+2}+c}=2\sqrt{{S}_{n+1}+c}$恒成立.
点评 本题考查等差数列的求和公式,考查学生分析解决问题的能力,确定c=$\frac{1}{2}$d是关键.

练习册系列答案
相关题目
6.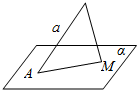 已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
 已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )| A. | 线段 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
5.已知f(x)在定义域(-4,1)上是减函数,且f(1+a)<f(3a-1),则a的取值范围是( )
| A. | (-∞,1) | B. | (-1,0) | C. | (-1,1) | D. | (0,1) |
5.函数f(x)=2x2-3|x|的递减区间是( )
| A. | [$\frac{3}{4}$,+∞) | B. | (-∞,-$\frac{3}{4}$] | C. | [-$\frac{3}{4}$,0]和[$\frac{3}{4}$,+∞) | D. | (-∞,-$\frac{3}{4}$],[0,$\frac{3}{4}$] |