题目内容
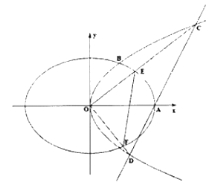
【题目】如图,抛物线![]() 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆![]() 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为![]() ,
,![]() 在第一象限的交点为
在第一象限的交点为![]() ,
,![]() 为坐标原点,且
为坐标原点,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.
①求证:![]() 恒为钝角;
恒为钝角;
②射线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点,记
两点,记![]() 的面积分别是
的面积分别是![]() ,问是否存在直线
,问是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)①证明见解析;② 存在,
;(2)①证明见解析;② 存在,![]() .
.
【解析】
试题分析:(1)由![]()
![]()
![]() .又
.又![]()
![]()
![]()
![]()
![]() .将点
.将点![]() 代入椭圆方程
代入椭圆方程![]()
![]()
![]() 椭圆为
椭圆为![]() ;(2)①设直线
;(2)①设直线![]() 的方程
的方程![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() 恒为钝角;②
恒为钝角;②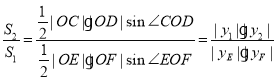 .由
.由![]() 的斜率为
的斜率为![]()
![]()
![]() :
:![]() .由
.由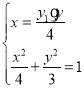
![]()
![]() 和
和![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 所求直线为
所求直线为![]() .
.
试题解析: (1)由![]() ,可得椭圆的长半轴
,可得椭圆的长半轴![]() .
.
∵![]() ,∴
,∴![]() ,代入抛物线求得
,代入抛物线求得![]() .
.
将点![]() 代入椭圆
代入椭圆![]() ,可得
,可得![]() ,
,
所以椭圆为![]() .
.
(2)①设直线![]() 的方程为
的方程为![]() ,由
,由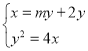 得
得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 恒为钝角;
恒为钝角;
②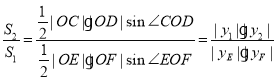 .
.
因为直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.
由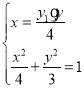 得
得![]() ,同理
,同理![]() ,
,
∴![]() ,
,
∴![]() ,
,
解之得:![]() ,所以所求直线为
,所以所求直线为![]() .
.

练习册系列答案
相关题目
