题目内容
将十进制数102转化为三进制数结果为: 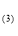
10210.
【解析】
试题分析:将十进制数转化为3进制数的方法为除3取余法,再把各步所得的余数从下到上排列即得10210.
考点:算法的应用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
题目内容
将十进制数102转化为三进制数结果为: 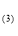
10210.
【解析】
试题分析:将十进制数转化为3进制数的方法为除3取余法,再把各步所得的余数从下到上排列即得10210.
考点:算法的应用.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案