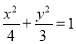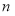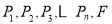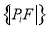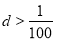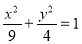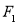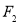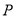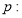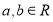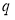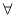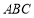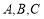题目内容
已知△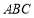 的两个顶点
的两个顶点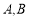 的坐标分别是
的坐标分别是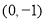 ,
,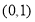 ,且
,且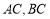 所在直线的斜率之积等于
所在直线的斜率之积等于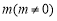 .
.
(1)求顶点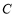 的轨迹
的轨迹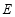 的方程,并判断轨迹
的方程,并判断轨迹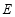 为何种圆锥曲线;
为何种圆锥曲线;
(2)当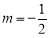 时,过点
时,过点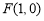 的直线
的直线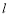 交曲线
交曲线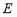 于
于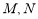 两点,设点
两点,设点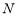 关于
关于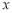 轴的对称点为
轴的对称点为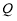 (
(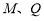 不重合), 试问:直线
不重合), 试问:直线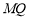 与
与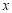 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
(1)详见解析;(2)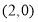 .
.
【解析】
试题分析:(1)设出顶点C的坐标,由AC,BC所在直线的斜率之积等于m(m≠0)列式整理得到顶点C的轨迹E的方程,然后分m的不同取值范围判断轨迹E为何种圆锥曲线;
(2)把 代入E得轨迹方程,由题意设出直线l的方程,和椭圆方程联立后利用根与系数关系求出M,N两点的横坐标的和与积,由两点式写出直线MQ的方程,取y=0后求出x,结合根与系数关系可求得x=2,则得到直线MQ与x轴的交点是定点,并求出定点..
代入E得轨迹方程,由题意设出直线l的方程,和椭圆方程联立后利用根与系数关系求出M,N两点的横坐标的和与积,由两点式写出直线MQ的方程,取y=0后求出x,结合根与系数关系可求得x=2,则得到直线MQ与x轴的交点是定点,并求出定点..
试题解析:(1)由题知: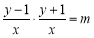
化简得: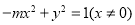 2分
2分
当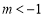 时 轨迹
时 轨迹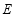 表示焦点在
表示焦点在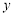 轴上的椭圆,且除去
轴上的椭圆,且除去 两点;
两点;
当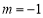 时 轨迹
时 轨迹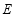 表示以
表示以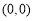 为圆心半径是1的圆,且除去
为圆心半径是1的圆,且除去 两点;
两点;
当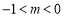 时 轨迹
时 轨迹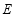 表示焦点在
表示焦点在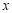 轴上的椭圆,且除去
轴上的椭圆,且除去 两点;
两点;
当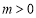 时 轨迹
时 轨迹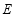 表示焦点在
表示焦点在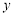 轴上的双曲线,且除去
轴上的双曲线,且除去 两点; 6分
两点; 6分
(2)设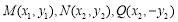
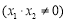
依题直线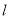 的斜率存在且不为零,则可设
的斜率存在且不为零,则可设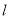 :
: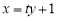 ,
,
代入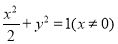 整理得
整理得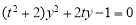
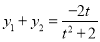 ,
,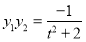 , 9分
, 9分
又因为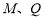 不重合,则
不重合,则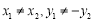
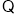
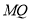 的方程为
的方程为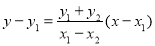 令
令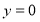 ,
,
得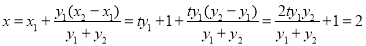
故直线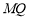 过定点
过定点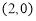 . 14分
. 14分
解二:设
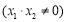
依题直线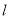 的斜率存在且不为零,可设
的斜率存在且不为零,可设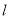 :
: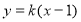
代入 整理得:
整理得: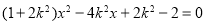
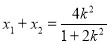 ,
,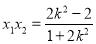 , 9分
, 9分
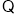
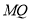 的方程为
的方程为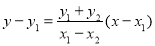 令
令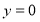 ,
,
得
 直线
直线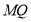 过定点
过定点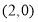 14分
14分
考点:1.椭圆的简单性质;2.与直线有关的动点轨迹方程.

练习册系列答案
相关题目