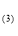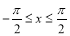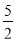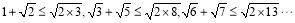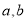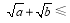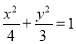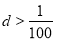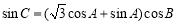Question

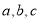在ABC中，三个内角A，B，C的对边分别为，且A，B，C成等差数列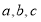，成等比数列，求证ABC为等边三角形.

 

Answer 1

证明过程详见试题解析.

【解析】

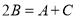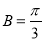试题分析：由已知条件可得,即；而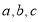成等比数列，得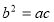，由余弦定理可得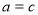，即 A=C ，所以 ABC为等边三角形.

试题解析：证明：由A，B，C成等差数列，有2B=A+C ①

因为A，B，C为ABC的内角，所以A+B+C=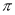 ②

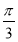由①②,得 B= ③

由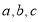成等比数列，有 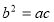④ 6分

由余弦定理及③，可得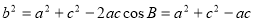

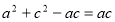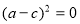再由④，得 即 因此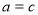

从而有A=C ⑤

由②③⑤，得A=B=C=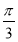

所以ABC为等边三角形.（本题为选修1-2 P37例3） 12分

考点：等差中项、等比中项、余弦定理.