题目内容
有一个不透明的袋子,装有4个完全相同的小球,球上分别编有数字1,2,3,4,
(1)若逐个不放回取球两次,求第一次取到球的编号为偶数且两个球的编号之和能被3整除的概率;
(2)若先从袋中随机取一个球,该球的编号为a,将球放回袋中,然后再从袋中随机取一个球,该球的编号为b,求直线ax+by+1=0与圆 有公共点的概率.
有公共点的概率.
(1)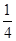 ;(2)
;(2)
解析试题分析:能理解放回抽样和不放回抽样中基本事件总数的变化是解该题的关键,(1)定义事件A=“第一次取到球的编号为偶数且两个球的编号之和能被3整除”,列举出逐个不放回取球两次的基本事件总数及第一次取到球的编号为偶数且两球编号能被3整除包含的基本事件数,代入古典概型概率的计算公式即可;
(2)定义事件B=“直线 与圆
与圆 有公共点”,列出基本事件总数及直线
有公共点”,列出基本事件总数及直线 与圆
与圆 有公共点包含的基本事件数,代入古典概型的概率计算公式即可.
有公共点包含的基本事件数,代入古典概型的概率计算公式即可.
试题解析:(1)记A=“第一次取到球的编号为偶数且两个球的编号之和能被3整除”,用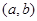 表示先后两次不放回取球所构成的基本事件,则基本事件有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12个,事件A包含的基本事件有(2,1),(2,4),(4,2)共三个,所以
表示先后两次不放回取球所构成的基本事件,则基本事件有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12个,事件A包含的基本事件有(2,1),(2,4),(4,2)共三个,所以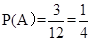 ;
;
(2)记B=“直线 与圆
与圆 有公共点”,基本事件有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共16个,依题意
有公共点”,基本事件有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共16个,依题意 ,即
,即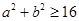 ,其中事件B包含的基本事件有(1,4),(2,4),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共8个,∴
,其中事件B包含的基本事件有(1,4),(2,4),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共8个,∴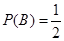
考点:1、直线和圆的位置关系;2、古典概型.

 经过坐标原点
经过坐标原点 和点
和点 ,且圆心在
,且圆心在 轴上.
轴上. 经过点
经过点 ,且
,且 ,求直线
,求直线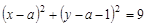 ,其中
,其中 为实常数.
为实常数. 被圆C截得的弦长为2,求
被圆C截得的弦长为2,求 ,0为坐标原点,若圆C上存在点M,使|MA|="2" |MO|,求
,0为坐标原点,若圆C上存在点M,使|MA|="2" |MO|,求 的取值范围.
的取值范围. ,直线
,直线 ,
, 。
。 取什么实数,直线
取什么实数,直线 与圆恒交于两点;
与圆恒交于两点; 截得的弦长最小时
截得的弦长最小时 是圆
是圆 上的点
上的点 的取值范围.
的取值范围. 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 截得的弦长是6.
截得的弦长是6.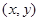 到定点
到定点 与到定点
与到定点 的距离之比为3.
的距离之比为3. ,若曲线C上恰有两个点到直线
,若曲线C上恰有两个点到直线 的距离为1,
的距离为1, 的取值范围。
的取值范围。 满足以下三个条件:(1)圆心在直线
满足以下三个条件:(1)圆心在直线 上,(2)与直线
上,(2)与直线 相切,(3)截直线
相切,(3)截直线 所得弦长为6。求圆
所得弦长为6。求圆 和点
和点 .
.
 向⊙
向⊙ 引切线
引切线 ,求直线
,求直线 截得的弦长为4的⊙
截得的弦长为4的⊙ 为(Ⅱ)中⊙
为(Ⅱ)中⊙ . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点 ,使得
,使得 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.