题目内容
已知动点M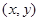 到定点
到定点 与到定点
与到定点 的距离之比为3.
的距离之比为3.
(Ⅰ)求动点M的轨迹C的方程,并指明曲线C的轨迹;
(Ⅱ)设直线 ,若曲线C上恰有两个点到直线
,若曲线C上恰有两个点到直线 的距离为1,
的距离为1,
求实数 的取值范围。
的取值范围。
(Ⅰ)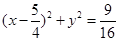 ,以
,以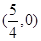 为圆心,
为圆心, 为半径的圆;
为半径的圆;
(Ⅱ)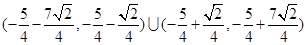
解析试题分析:(Ⅰ)设点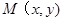 ,由已知得
,由已知得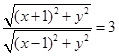 ,化简,得动点
,化简,得动点 的轨迹方程,并说明轨迹类型;(Ⅱ)平面内到定直线的距离等于1的点在两条与已知直线平行,且距离等于1的平行线上,∴只需让曲线
的轨迹方程,并说明轨迹类型;(Ⅱ)平面内到定直线的距离等于1的点在两条与已知直线平行,且距离等于1的平行线上,∴只需让曲线 与这两条平行线有两个公共点即可,当由图得圆心
与这两条平行线有两个公共点即可,当由图得圆心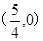 到直线
到直线 的距离
的距离 时,圆上有一个点到直线的距离等于1,直线向上移时圆上有两个点到直线距离等于1,当
时,圆上有一个点到直线的距离等于1,直线向上移时圆上有两个点到直线距离等于1,当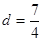 ,圆上有1个点到直线距离等于1,继续向上移动时圆上无满足条件的点,∴满足
,圆上有1个点到直线距离等于1,继续向上移动时圆上无满足条件的点,∴满足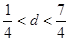 ,即
,即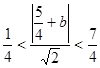 ,解不等式可得
,解不等式可得 的取值范围.
的取值范围.
试题解析:(Ⅰ) 解;设点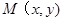 ,由已知可得
,由已知可得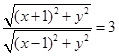 2分
2分
整理得: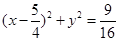 即为M的轨迹方程 4分
即为M的轨迹方程 4分
曲线C的轨迹是以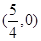 为圆心,
为圆心, 为半径的圆 6分
为半径的圆 6分
(Ⅱ)设圆心到直线 的距离为
的距离为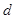 ,当
,当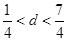 时,符合题意 8分
时,符合题意 8分 ,即
,即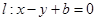 ,
,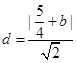
当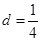 时,
时, 9分
9分
当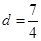 时,
时,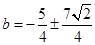 10分
10分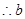 的取值范围是:
的取值范围是: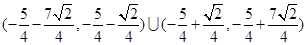 12分
12分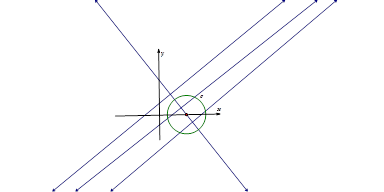
考点:1、点到直线的距离;2、曲线的轨迹方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的圆心在直线
的圆心在直线 上,且与
上,且与 轴交于两点
轴交于两点 ,
, .
.
 的圆
的圆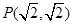 ,且与圆B:
,且与圆B: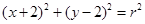
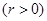 关于直线
关于直线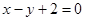 对称.
对称.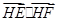 的最小值。
的最小值。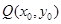 向圆A和圆B各引一条切线,切点分别为C、D,设
向圆A和圆B各引一条切线,切点分别为C、D,设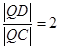 ,求证:平面上存在一定点M使得Q到M的距离为定值,并求出该定值.
,求证:平面上存在一定点M使得Q到M的距离为定值,并求出该定值.  有公共点的概率.
有公共点的概率. 直线
直线
 取何实数,直线
取何实数,直线 与圆C恒相交;
与圆C恒相交; 与圆C:
与圆C: ,
, 相切,求m的值。
相切,求m的值。 ,求圆C 截直线L所得的弦长。
,求圆C 截直线L所得的弦长。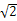 ,在
,在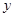 轴上截得线段长为
轴上截得线段长为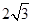 .
. ,求圆P的方程.
,求圆P的方程. ,直线
,直线 过定点
过定点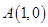 .
. 的坐标和圆的半径
的坐标和圆的半径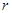 ;
; 面积的最大值,并求此时
面积的最大值,并求此时 、
、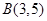 两点,且圆心C在直线
两点,且圆心C在直线 上.
上.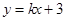 与⊙C总有公共点,求实数
与⊙C总有公共点,求实数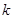 的取值范围.
的取值范围.