题目内容

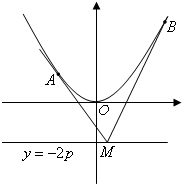精英家教网如图，设抛物线x2=2py（p＞0），M为直线y=-2p上任意一点，过M引抛物线的切线，切点分别为A，B．求证：A，M，B三点的横坐标成等差数列．
分析：设出A，B的坐标，对抛物线的方程进行求导，求得AM和BM的斜率，因此可表示出MA的直线方程和直线MB的方程，联立求得2x0=x1+x2．判断出三者的横坐标成等差数列．
解答：证明：由题意，设A（x1，
x12
2p
），B（x2，
x22
2p
）（x1＜x2），M（x0，-2p）．
由x2=2py得y=
x2
2p
，得y′=
x
p
，
所以kMA=
x1
p
，kMB=
x2
p
．
因此直线MA的方程为y+2p=
x1
p
(x-x0)，直线MB的方程为y+2p=
x2
p
(x-x0)．
所以，
x12
2p
+2p=
x1
p
(x-x0)①，
x22
2p
+2p=
x2
p
(x-x0)②
由①、②得
x1+x2
2
=x1+x2-x0，因此x0=
x1+x2
2
，即2x0=x1+x2．
所以A，M，B三点的横坐标成等差数列．
点评：本题主要考查了直线与圆锥曲线的综合问题，考查学生知识的灵活运用的能力和基本的计算的能力，属于中档题．
练习册系列答案
相关题目
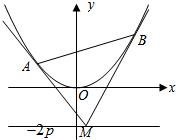精英家教网如图，设抛物线方程为x2=2py（p＞0），M为直线y=-2p上任意一点，过M引抛物线的切线，切点分别为A，B．
（Ⅰ）求证：A，M，B三点的横坐标成等差数列；
（Ⅱ）已知当M点的坐标为（2，-2p）时，|AB|=4
10
．求此时抛物线的方程；
（Ⅲ）是否存在点M，使得点C关于直线AB的对称点D在抛物线x2=2py（p＞0）上，其中，点C满足
OC
=
OA
+
OB
（O为坐标原点）．若存在，求出所有适合题意的点M的坐标；若不存在，请说明理由．
精英家教网如图，设抛物线C：y=x2的焦点为F，动点P在直线l：x-y-2=0上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点．则△APB的重心G的轨迹方程为
 
．
精英家教网如图，设抛物线方程为x2=2py（p＞0），M为直线y=-2p上任意一点，过M引抛物线的切线，切点分别为A，B．
（Ⅰ）求证：A，M，B三点的横坐标成等差数列；
（Ⅱ）已知当M点的坐标为（2，2p）时，|AB|=4
10
，求此时抛物线的方程．
如图，过抛物线x2=4y的对称轴上任一点P（0，m）（m＞0）作直线与抛物线交于A（x1，y1），B（x2，y2）两点．
（I）若
AP
=λ
PB
(λ∈R)，证明：λ=-
x1
x2
；
（II）在（I）条件下，若点Q是点P关于原点对称点，证明：
QP
⊥(
QA
-λ
QB
)；
（III）设直线AB的方程是x-2y+12=0，过A，B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网