题目内容
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.(I)若
| AP |
| PB |
| x1 |
| x2 |
(II)在(I)条件下,若点Q是点P关于原点对称点,证明:
| QP |
| QA |
| QB |
(III)设直线AB的方程是x-2y+12=0,过A,B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
分析:(I)利用向量相等
=λ
(λ∈R),即可证明;
(II)依题意,可设直线AB的方程为y=kx+m,代入抛物线方程,得到根与系数的关系,点Q是点P关于原点的称点,故点Q(0,-m),从而
=(0,2m),进而得到
-λ
,利用根与系数的关系及其数量积运算即可得出
•(
-λ
)=0即可证明
⊥(
-λ
).
(III)直线AB的方程与抛物线方程联立即可解得点A,B的坐标,利用导数即可切线的斜率,再利用圆的切线的性质及圆的标准方程即可解得.
| AP |
| PB |
(II)依题意,可设直线AB的方程为y=kx+m,代入抛物线方程,得到根与系数的关系,点Q是点P关于原点的称点,故点Q(0,-m),从而
| QP |
| QA |
| QB |
| QP |
| QA |
| QB |
| QP |
| QA |
| QB |
(III)直线AB的方程与抛物线方程联立即可解得点A,B的坐标,利用导数即可切线的斜率,再利用圆的切线的性质及圆的标准方程即可解得.
解答:解:(I)∵
=λ
(λ∈R),∴-x1=λx2,(x2≠0),即λ=-
.
(II)依题意,可设直线AB的方程为y=kx+m,
代入抛物线方程x2=4y得x2-4kx-4m=0 ①
∵直线与抛物线交于A(x1,y1),B(x2,y2)两点.
∴x1x2=-4m.
点Q是点P关于原点的称点,
故点Q(0,-m),从而
=(0,2m),
∴
-λ
=(x1,y1+m)-λ(x2,y2+m)=(x1-λx2,y1-λy2+(1-λ)m),
∴
•(
-λ
)=2m[y1-λy2+(1-λ)m]=2m[
+
•
+(1+
)m]=2m[
-m+m+
]=2mx1•
=0
∴
⊥(
-λ
).
(III)由
得点A、B坐标分别是(6,9)、(-4,4),
由x2=4y得y=
x2,∴y′=
x,
所以抛物线x2=4y在点A处切线的斜率为y′|x=6=3.
设圆C的方程是(x-a)2+(y-b)2=r2
则
,
解之得a=-
,b=
,r2=(a+4)2+(b-4)2=
,
即x2+y2+3x-23y+72=0.
| AP |
| PB |
| x1 |
| x2 |
(II)依题意,可设直线AB的方程为y=kx+m,
代入抛物线方程x2=4y得x2-4kx-4m=0 ①
∵直线与抛物线交于A(x1,y1),B(x2,y2)两点.
∴x1x2=-4m.
点Q是点P关于原点的称点,
故点Q(0,-m),从而
| QP |
∴
| QA |
| QB |
∴
| QP |
| QA |
| QB |
| ||
| 4 |
| x1 |
| x2 |
| ||
| 4 |
| x1 |
| x2 |
| ||
| 4 |
| mx1 |
| x2 |
| x1x2+4m |
| 4x2 |
∴
| QP |
| QA |
| QB |
(III)由
|
由x2=4y得y=
| 1 |
| 4 |
| 1 |
| 2 |
所以抛物线x2=4y在点A处切线的斜率为y′|x=6=3.
设圆C的方程是(x-a)2+(y-b)2=r2
则
|
解之得a=-
| 3 |
| 2 |
| 23 |
| 2 |
| 125 |
| 2 |
即x2+y2+3x-23y+72=0.
点评:本题综合考查了抛物线与圆的标准方程及其性质、直线与抛物线相交问题转化为方程联立得到根与系数的关系、直线与圆及抛物线相切问题、利用导数的几何意义得到切线的斜率、斜率的计算公式、切线的性质等解出知识与基本技能,考查了推理能力与计算能力.

练习册系列答案
相关题目
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.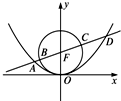 如图,过抛物线x2=4y焦点的直线依次交抛物线与圆x2+(y-1)2=1于点A、B、C、D,则
如图,过抛物线x2=4y焦点的直线依次交抛物线与圆x2+(y-1)2=1于点A、B、C、D,则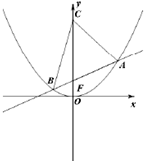 (2012•绍兴模拟)如图,过抛物线x2=4y焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1).
(2012•绍兴模拟)如图,过抛物线x2=4y焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1). 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点. 所成的比为λ,证明:
所成的比为λ,证明: