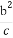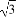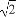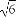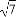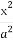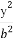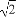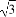题目内容
已知双曲线mx2-ny2=1(m>0,n>0)的离心率为2,则椭圆mx2+ny2=1的离心率为( )
(A) (B)
(B)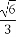 (C)
(C)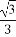 (D)
(D)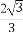
B
【解析】由已知双曲线的离心率为2,得:
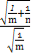 =2,
=2,
解得m=3n,又m>0,n>0,
∴m>n,即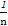 >
>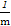 ,
,
故由椭圆mx2+ny2=1得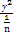 +
+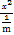 =1.
=1.
∴所求椭圆的离心率为e=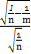 =
=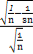 =
=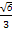 .
.
【误区警示】本题极易造成误选而失分,根本原因是由于将椭圆mx2+ny2=1焦点所在位置弄错,从而把a求错造成

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目