题目内容
已知离心率为 的椭圆C1的左、右焦点分别为F1,F2,抛物线C2:y2=4mx(m>0)的焦点为F2,设椭圆C1与抛物线C2的一个交点为P(x',y'),
的椭圆C1的左、右焦点分别为F1,F2,抛物线C2:y2=4mx(m>0)的焦点为F2,设椭圆C1与抛物线C2的一个交点为P(x',y'),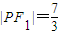 ,则椭圆C1的标准方程为 ;抛物线C2的标准方程为 .
,则椭圆C1的标准方程为 ;抛物线C2的标准方程为 .
【答案】分析:根据题意设出椭圆的方程,把椭圆的方程与抛物线的方程进行联立,得到交点的坐标,|PF1|的长,求出m的值,求写出椭圆的方程、抛物线C2的标准方程,得到结果.
解答: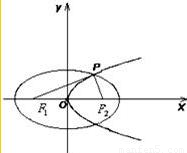 解:因为c=m,e=
解:因为c=m,e= ,
,
∴a=2m,b2=3m2,设椭圆方程为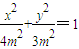 ,
,
由椭圆的方程与y2=4mx,得3x2+16mx-12m2=0
即(x+6m)(3x-2m)=0,得x1=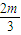 ,
,
代入抛物线方程得y=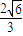 m,P(
m,P( 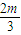 ,
,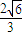 m)
m)
|PF2|=x1+m=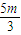 ,
,
|PF1|=2a-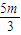 =
=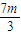 =
= ,
,
∴m=1,
当m=1时,椭圆C1的标准方程为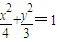 ;抛物线C2的标准方程为 y2=4x.
;抛物线C2的标准方程为 y2=4x.
故答案为: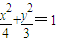 ;y2=4x.
;y2=4x.
点评:本题考查解析几何与数列的综合题目,题目中所应用的数列的解题思想,用到曲线与曲线之间的交点问题,本题主要考查运算,整个题目的解答过程看起来非常繁琐,注意运算.
解答:
 解:因为c=m,e=
解:因为c=m,e= ,
,∴a=2m,b2=3m2,设椭圆方程为
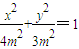 ,
,由椭圆的方程与y2=4mx,得3x2+16mx-12m2=0
即(x+6m)(3x-2m)=0,得x1=
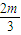 ,
,代入抛物线方程得y=
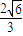 m,P(
m,P( 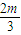 ,
,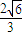 m)
m)|PF2|=x1+m=
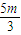 ,
,|PF1|=2a-
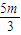 =
=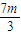 =
= ,
,∴m=1,
当m=1时,椭圆C1的标准方程为
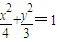 ;抛物线C2的标准方程为 y2=4x.
;抛物线C2的标准方程为 y2=4x.故答案为:
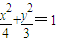 ;y2=4x.
;y2=4x.点评:本题考查解析几何与数列的综合题目,题目中所应用的数列的解题思想,用到曲线与曲线之间的交点问题,本题主要考查运算,整个题目的解答过程看起来非常繁琐,注意运算.

练习册系列答案
相关题目
 的椭圆C:
的椭圆C: 过(1,
过(1, )
) 的椭圆C:
的椭圆C: +
+ =1(a>b>0)过点M(
=1(a>b>0)过点M( ,1,O是坐标原点.
,1,O是坐标原点. ⊥
⊥ ,判定直线AB与圆O:x2+y2=
,判定直线AB与圆O:x2+y2= 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. 为的椭圆C:
为的椭圆C: (a>b>0)与过点A(5,0),B(0,
(a>b>0)与过点A(5,0),B(0, )的直线有且只有一个公共点M.
)的直线有且只有一个公共点M. ,若存在,求出直线l的方程;若不存在,请说明理由.
,若存在,求出直线l的方程;若不存在,请说明理由. 的椭圆C:
的椭圆C: 的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为
的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为 .
. .试探究
.试探究 的取值范围.
的取值范围.