题目内容
已知圆C: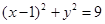 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线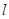 交圆C于A、B两点。
交圆C于A、B两点。
(1)当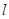 经过圆心C时,求直线
经过圆心C时,求直线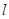 的方程;
的方程;
(2)当弦AB的长为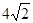 时,写出直线
时,写出直线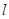 的方程。
的方程。
【答案】
(1)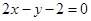 。 (2)直线l的方程为
。 (2)直线l的方程为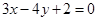 或
或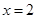 。
。
【解析】
试题分析:(1)圆心坐标为(1,0),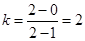 ,
,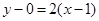 ,整理得
,整理得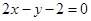 。
。
(2)圆的半径为3,当直线l的斜率存在时,设直线l的方程为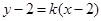 ,整理得
,整理得
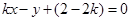 ,圆心到直线l的距离为
,圆心到直线l的距离为
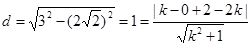 ,
,
解得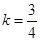 ,代入整理得
,代入整理得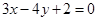 。
。
当直线l的斜率不存在时,直线l的方程为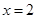 ,经检验符合题意。
,经检验符合题意。
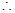 直线l的方程为
直线l的方程为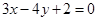 或
或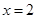 。
。
考点:本题主要考查直线与圆的位置关系,点到直线的距离公式。
点评:易错题,涉及直线与圆相交问题,往往要利用圆的特征三角形,通过弦长的一半、圆心到直线的距离、半径之间的关系,达到解题目的。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
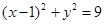 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线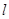 交圆C于A、B两点。
交圆C于A、B两点。 时,写出直线
时,写出直线 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线 交圆C于A、B两点.
交圆C于A、B两点. 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点. 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线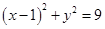 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.