题目内容
(本小题满分9分)已知圆C: 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(Ⅰ)当l经过圆心C时,求直线l的方程;
(Ⅱ)当弦AB被点P平分时,写出直线l的方程;
(Ⅲ)当直线l的倾斜角为45º时,求弦AB的长.
【答案】
解:(1)已知圆C: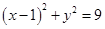 的圆心为C(1,0),因直线过点P、C,所以直线l的斜率为2,直线l的方程为y=2(x-1),即 2x-y-20.
的圆心为C(1,0),因直线过点P、C,所以直线l的斜率为2,直线l的方程为y=2(x-1),即 2x-y-20.
(2)当弦AB被点P平分时,l⊥PC, 直线l的方程为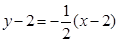 , 即 x+2y-6=0
, 即 x+2y-6=0
(3)当直线l的倾斜角为45º时,斜率为1,直线l的方程为y-2=x-2 ,即 x-y=0,
圆心C到直线l的距离为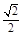 ,圆的半径为3,弦AB的长为
,圆的半径为3,弦AB的长为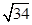 .
.
【解析】略

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 ,
,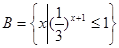 ,求(
,求( RA)
RA)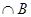
 ,
, 是同一平面内的两个向量,其中
是同一平面内的两个向量,其中 ,
, 且
且 与
与 垂直,(1)求
垂直,(1)求 ;
; 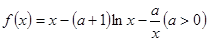 。
。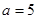 时,求函数
时,求函数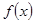 的单调递增区间;
的单调递增区间; ,函数
,函数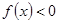 在
在 上恒成立。
上恒成立。