题目内容
已知圆C：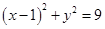
内有一点P（2，2），过点P作直线l交圆C于A、B两点.
（1）当l经过圆心C时，求直线l的方程；
（2）当弦AB被点P平分时，写出直线l的方程
【答案】
（1）2x-y-2=0
（2）x+2y-6=0
【解析】(1)已知圆C：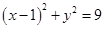
的圆心为C（1，0），因直线过点P、C，所以直线l斜率为2，直线l的方程为y=2(x-1),即
2x-y-2=0.
(2)当弦AB被点P平分时，l⊥PC, 直线l的方程为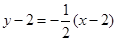
, 即
x+2y-6=0
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
内有一点P（2，2），过点P作直线
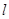交圆C于A、B两点。
时，写出直线
内有一点P（2，2），过点P作直线
交圆C于A、B两点.
内有一点P（2，2），过点P作直线l交圆C于A、B两点.
内有一点P（2，2），过点P作直线