题目内容
.(本题满分13分)已知圆C: 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
l交圆C于A、B两点.
(1) 当l经过圆心C时,求直线l的方程;
(2) 当弦AB被点P平分时,写出直线l的方程;
(3) 当直线l的倾斜角为45º时,求弦AB的长.
【答案】
解:
(1) 已知圆C: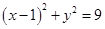 的圆心为C(1,0),因直线过点P、C,所以直线l的斜率2
的圆心为C(1,0),因直线过点P、C,所以直线l的斜率2
直线l的方程为y=2(x-1),即 2x-y-2=0. …………………………………4分
(2) 当弦AB被点P平分时,l⊥PC, 直线l的方程为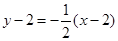 , 即
, 即
x+2y-6=0………8分
(3) 当直线l的倾斜角为45º时,斜率为1,直线l的方程为y-2=x-2 ,即 x-y=0
圆心C到直线l的距离为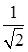 ,圆的半径为3,
,圆的半径为3,
弦AB的长为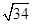 .……………………………………………13分
.……………………………………………13分
【解析】略

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.