题目内容
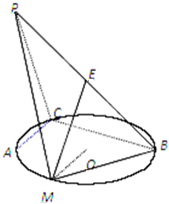 (2012•海淀区二模)如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=
(2012•海淀区二模)如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=| π | 3 |
(Ⅰ)求证:平面MOE∥平面PAC;
(Ⅱ)求证:平面PAC⊥平面PCB;
(Ⅲ)设二面角M-BP-C的大小为θ,求cosθ的值.
分析:(Ⅰ)先证明OE∥平面PAC、OM∥平面PAC,再利用面面平行的判定,可得平面MOE∥平面PAC;
(Ⅱ)证明BC⊥平面PAC,利用面面垂直的判定,可得平面PAC⊥平面PCB;
(Ⅲ)求出S△PBC、S△PMB,利用面积比,即可求出二面角M-BP-C的大小.
(Ⅱ)证明BC⊥平面PAC,利用面面垂直的判定,可得平面PAC⊥平面PCB;
(Ⅲ)求出S△PBC、S△PMB,利用面积比,即可求出二面角M-BP-C的大小.
解答:(Ⅰ)证明:因为点E为线段PB的中点,点O为线段AB的中点,所以OE∥PA
因为PA?平面PAC,OE?平面PAC,所以OE∥平面PAC.
因为OM∥AC,因为AC?平面PAC,OM?平面PAC,所以OM∥平面PAC.
因为OE∩OM=O,所以平面MOE∥平面PAC;
(Ⅱ)证明:因为PA⊥平面ABC,BC?平面ABC,所以PA⊥BC,
因为点C在以AB为直径的⊙O上,所以BC⊥AC
因为PA∩AC=A,所以BC⊥平面PAC
因为BC?平面PCB,所以平面PAC⊥平面PCB;
(Ⅲ)解:∵∠CBA=
,PA=AB=2,∴BC=1,AC=
,PC=
,
∵BC⊥PC,∴S△PBC=
×1×
=
由AM2=1+1-2×1×1×cos30°=2-
,∴PM2=6-
,∴BM2=2+
,
∴S△PMB=
∵二面角M-BP-C的大小为θ,
∴利用面积射影定理可得cosθ=
=
.
因为PA?平面PAC,OE?平面PAC,所以OE∥平面PAC.
因为OM∥AC,因为AC?平面PAC,OM?平面PAC,所以OM∥平面PAC.
因为OE∩OM=O,所以平面MOE∥平面PAC;
(Ⅱ)证明:因为PA⊥平面ABC,BC?平面ABC,所以PA⊥BC,
因为点C在以AB为直径的⊙O上,所以BC⊥AC
因为PA∩AC=A,所以BC⊥平面PAC
因为BC?平面PCB,所以平面PAC⊥平面PCB;
(Ⅲ)解:∵∠CBA=
| π |
| 3 |
| 3 |
| 7 |
∵BC⊥PC,∴S△PBC=
| 1 |
| 2 |
| 7 |
| ||
| 2 |
由AM2=1+1-2×1×1×cos30°=2-
| 3 |
| 3 |
| 3 |
∴S△PMB=
| 1 |
| 2 |
9+4
|
∵二面角M-BP-C的大小为θ,
∴利用面积射影定理可得cosθ=
| ||||||
|
| ||||
|
点评:本题考查面面平行,考查线面垂直,考查面面角,解题的关键是掌握面面平行、面面垂直的判定方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目