题目内容
（2012•海淀区二模）已知点F1、F2是椭圆x2+2y2=2的两个焦点，点P是该椭圆上的一个动点，那么|
+
|的最小值是（ ）
| PF1 |
| PF2 |
分析：根据向量的加法法则和三角形中线的性质，可得|
+
|等于点P到原点距离的2倍，由此结合椭圆的标准方程和简单几何性质，即可得到|
+
|的最小值是2．
| PF1 |
| PF2 |
| PF1 |
| PF2 |
解答：解：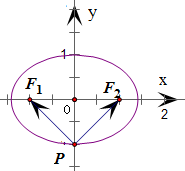
∵O为F1F2的中点，
∴
+
=2
，可得|
+
|=2|
|
当点P到原点的距离最小时，|
|达到最小值，|
+
|同时达到最小值．
∵椭圆x2+2y2=2化成标准形式，得
+y2=1
∴a2=2且b2=1，可得a=
，b=1
因此点P到原点的距离最小值为短轴一端到原点的距离，即|
|最小值为b=1
∴|
+
|=2|
|的最小值为2
故选：C
∵O为F1F2的中点，∴
| PF1 |
| PF2 |
| PO |
| PF1 |
| PF2 |
| OP |
当点P到原点的距离最小时，|
| OP |
| PF1 |
| PF2 |
∵椭圆x2+2y2=2化成标准形式，得
| x2 |
| 2 |
∴a2=2且b2=1，可得a=
| 2 |
因此点P到原点的距离最小值为短轴一端到原点的距离，即|
| OP |
∴|
| PF1 |
| PF2 |
| OP |
故选：C
点评：本题给出点F1、F2是椭圆的两个焦点，求椭圆上一个动点P指向两个焦点所成向量的和向量长度的最小值，着重考查了椭圆的标准方程与简单几何性质等知识，属于基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目