题目内容
【题目】已知椭圆C: ![]() =1(a>b>0),e=
=1(a>b>0),e= ![]() ,其中F是椭圆的右焦点,焦距为2,直线l与椭圆C交于点A、B,点A,B的中点横坐标为
,其中F是椭圆的右焦点,焦距为2,直线l与椭圆C交于点A、B,点A,B的中点横坐标为 ![]() ,且
,且 ![]() =λ
=λ ![]() (其中λ>1).
(其中λ>1).
(1)求椭圆C的标准方程;
(2)求实数λ的值.
【答案】
(1)解:由条件可知c=1,a=2,故b2=a2﹣c2=3,
椭圆的标准方程是 ![]() .
.
(2)解:由 ![]() ,可知A,B,F三点共线,设A(x1,y1),B(x2,y2),
,可知A,B,F三点共线,设A(x1,y1),B(x2,y2),
若直线AB⊥x轴,则x1=x2=1,不合题意.
当AB所在直线l的斜率k存在时,设方程为y=k(x﹣1).
由  ,消去y得(3+4k2)x2﹣8k2x+4k2﹣12=0.①
,消去y得(3+4k2)x2﹣8k2x+4k2﹣12=0.①
由①的判别式△=64k4﹣4(4k2+3)(4k2﹣12)=144(k2+1)>0.
因为  ,
,
所以 ![]() =
= ![]() ,所以
,所以 ![]() .
.
将 ![]() 代入方程①,得4x2﹣2x﹣11=0,
代入方程①,得4x2﹣2x﹣11=0,
解得x= ![]() .
.
又因为 ![]() =(1﹣x1,﹣y1),
=(1﹣x1,﹣y1), ![]() =(x2﹣1,y2),
=(x2﹣1,y2), ![]() ,
,
![]() ,解得
,解得 ![]()
【解析】(1)由条件可知c=1,a=2,由此能求出椭圆的标准方程.(2)由 ![]() ,可知A,B,F三点共线,设A(x1 , y1),B(x2 , y2),直线AB⊥x轴,则x1=x2=1,不合意题意.当AB所在直线l的斜率k存在时,设方程为y=k(x﹣1).由
,可知A,B,F三点共线,设A(x1 , y1),B(x2 , y2),直线AB⊥x轴,则x1=x2=1,不合意题意.当AB所在直线l的斜率k存在时,设方程为y=k(x﹣1).由  ,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根的判别式、韦达定理,结合已知条件能求出实数λ的值.
,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根的判别式、韦达定理,结合已知条件能求出实数λ的值.

 名校课堂系列答案
名校课堂系列答案【题目】在一次抽样调查中测得样本的6组数据,得到一个变量![]() 关于
关于![]() 的回归方程模型,其对应的数值如下表:
的回归方程模型,其对应的数值如下表:
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)请用相关系数![]() 加以说明
加以说明![]() 与
与![]() 之间存在线性相关关系(当
之间存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)根据(1)的判断结果,建立![]() 关于
关于![]() 的回归方程并预测当
的回归方程并预测当![]() 时,对应的
时,对应的![]() 值为多少(
值为多少(![]() 精确到
精确到![]() ).
).
附参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
,![]() ,相关系数
,相关系数![]() 公式为:
公式为: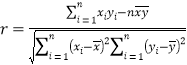 .
.
参考数据:
![]() ,
,![]() ,
,![]() ,
,![]() .
.

