题目内容
【题目】某市在创建国家级卫生城(简称“创卫”)的过程中,相关部门需了解市民对“创卫”工作的满意程度,若市民满意指数不低于0.8(注:满意指数![]()
![]() ),“创卫”工作按原方案继续实施,否则需进一步整改.为此该部门随机调查了100位市民,根据这100位市民给“创卫”工作的满意程度评分,按以下区间:
),“创卫”工作按原方案继续实施,否则需进一步整改.为此该部门随机调查了100位市民,根据这100位市民给“创卫”工作的满意程度评分,按以下区间:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分为六组,得到如图频率分布直方图:
分为六组,得到如图频率分布直方图:
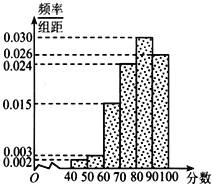
(1)为了解部分市民给“创卫”工作评分较低的原因,该部门从评分低于60分的市民中随机选取2人进行座谈,求这2人所给的评分恰好都在![]() 的概率;
的概率;
(2)根据你所学的统计知识,判断该市“创卫”工作是否需要进一步整改,并说明理由.
【答案】(1)![]() ;(2)该市“创卫”工作不需要进一步整改
;(2)该市“创卫”工作不需要进一步整改
【解析】
(1)由频率分布直方图分别求得评分在![]() 和
和![]() 的市民人数,根据古典概型可求得结果;
的市民人数,根据古典概型可求得结果;
(2)由频率分布直方图估计平均数的方法计算得到满意程度平均分,从而求得满意指数,得到判断结果.
(1)由频率分布直方图知:评分在![]() 的市民人数为
的市民人数为![]() 人;评分在
人;评分在![]() 的市民人数为
的市民人数为![]() 人
人
![]() 从评分低于
从评分低于![]() 分的市民中选取
分的市民中选取![]() 人,
人,![]() 人所给评分都在
人所给评分都在![]() 的概率
的概率![]()
(2)由频率分布直方图可得满意程度平均分为:
![]()
![]() 满意指数
满意指数![]()
![]() 该市“创卫”工作不需要进一步整改
该市“创卫”工作不需要进一步整改

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查.现在按课外阅读时间的情况将学生分成三类:![]() 类(不参加课外阅读),
类(不参加课外阅读),![]() 类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),
类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),![]() 类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
|
|
| |
男生 |
| 5 | 3 |
女生 |
| 3 | 3 |
(1)求出表中![]() ,
,![]() 的值;
的值;
(2)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | ||
不参加课外阅读 | ||||
参加课外阅读 | ||||
总计 |
P(K≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |