题目内容
 的内角
的内角 所对的边分别为
所对的边分别为 .
.
(1)若 成等差数列,证明:
成等差数列,证明: ;
;
(2)若 成等比数列,求
成等比数列,求 的最小值.
的最小值.
(1)证明见解析;(2)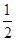 .
.
解析试题分析:(1)因为 成等差数列,所以
成等差数列,所以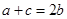 ,再由三角形正弦定理得
,再由三角形正弦定理得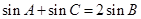 ,又在
,又在 中,有
中,有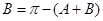 ,所以
,所以 ,最后得:
,最后得: ,即得证;
,即得证;
(2)因为 成等比数列,所以
成等比数列,所以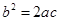 ,由余弦定理得
,由余弦定理得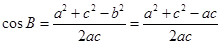
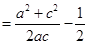 ,根据基本不等式
,根据基本不等式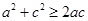 (当且仅当
(当且仅当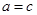 时等号成立)得
时等号成立)得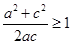 (当且仅当
(当且仅当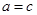 时等号成立),即得
时等号成立),即得 ,所以
,所以 的最小值为
的最小值为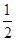
试题解析:(1)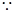
 成等差数列
成等差数列
由正弦定理得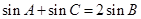

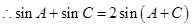
(2)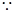
 成等比数列
成等比数列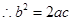
由余弦定理得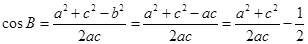
 (当且仅当
(当且仅当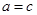 时等号成立)
时等号成立)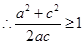 (当且仅当
(当且仅当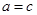 时等号成立)
时等号成立) (当且仅当
(当且仅当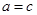 时等号成立)
时等号成立)
即
所以 的最小值为
的最小值为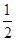
考点:正弦定理;余弦定理;基本不等式.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
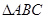 中,
中,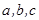 分别是角A、B、C的对边,
分别是角A、B、C的对边, 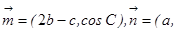
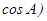 ,且
,且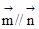 .
.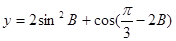 的值域.
的值域. 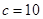 , 又知
, 又知 ,求边
,求边 、
、 的长.
的长.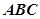 中,角
中,角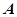 、
、 、
、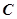 的对边分别为
的对边分别为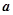 、
、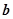 、
、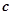 ,且
,且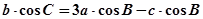 .
.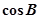 ;
;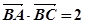 ,且
,且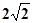 ,求
,求 ,函数
,函数 .
. 的对称中心;
的对称中心;  中,
中, 分别是角
分别是角 对边,且
对边,且 ,且
,且 ,求
,求 的取值范围.
的取值范围. 两地连线上的定点
两地连线上的定点 处建造广告牌
处建造广告牌 ,其中
,其中 为顶端,
为顶端, 长35米,
长35米, 长80米,设
长80米,设 和
和 看
看 .
.
 ,问
,问 求
求 中,
中, .
.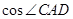 的值;
的值; ,
, ,求
,求 的长.
的长.
 的三内角
的三内角 、
、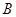 、
、 所对的边分别是
所对的边分别是 ,
, ,
, ,向量
,向量
 ,且
,且 。
。 ,求
,求 的范围。
的范围。