题目内容
3.一个几何体的三视图如图所示,则这个几何体的表面积等于10+2$\sqrt{3}$+4$\sqrt{2}$.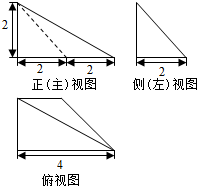
分析 该几何体是四棱锥,底面是直角梯形,一条侧棱垂直底面,根据公式可求表面积.
解答 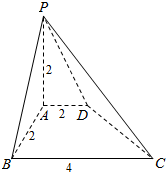 解:由三视图复原几何体,如图所示:
解:由三视图复原几何体,如图所示:
它的底面是直角梯形,一条侧棱垂直底面高为2,
故底面梯形ABCD的面积为:6,
后侧面△PAD的面积为:2,
左侧面△PAB的面积为:2,
前侧面△PBC的面积为:$\frac{1}{2}×PB×BC$=4$\sqrt{2}$,
右侧面△PCD中PD=CD=2$\sqrt{2}$,PC=$2\sqrt{6}$,
故PC上的高长为:$\sqrt{2}$,
则右侧面△PCD的面积为:$\frac{1}{2}×2\sqrt{6}×\sqrt{2}$=2$\sqrt{3}$,
故几何体的表面积S=10+2$\sqrt{3}$+4$\sqrt{2}$,
故答案为:10+2$\sqrt{3}$+4$\sqrt{2}$
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
17.盒中装有8个零件,其中有2个次品,现从中随机抽取2个,则恰有1个次品的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{3}$ |
14.设F1、F2分别是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则PM+PF1的最大值为15.
18.给定映射f:(x,y)→(2x+y,x-2y),在映射f下,(3,-1)的原像为( )
| A. | (-1,3) | B. | (5,5) | C. | (3,-1) | D. | (1,1) |
8.下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的是( )
| A. | $y=\frac{1}{x}$ | B. | y=-2|x| | C. | $y={log_3}{x^2}$ | D. | y=x-x2 |
12.已知数列{an}满足a1=1,an•an+1=2n,则$\frac{{{a_{2016}}}}{{{a_{2015}}}}$=( )
| A. | 2 | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{1}{2}$ |
13.已知函数f(x)=sin2x,为了得到g(x)=cos2x的图象,只要将y=f(x)的图象( )
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向右平移$\frac{π}{2}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
