题目内容
19.在区间(0,2]里任取两个数x、y,分别作为点P的横、纵坐标,则点P到点A(-1,1)的距离小于$\sqrt{2}$的概率为( )| A. | $\frac{4-π}{8}$ | B. | $\frac{π-2}{4}$ | C. | $\frac{4-π}{4}$ | D. | $\frac{π-2}{8}$ |
分析 根据几何概型的概率公式求出对应事件的面积即可得到结论.
解答 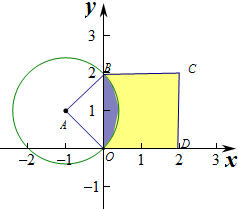 解:设P(x,y),
解:设P(x,y),
由|PA|$<\sqrt{2}$得$\sqrt{(x+1)^{2}+(y-1)^{2}}<\sqrt{2}$,
即(x+1)2+(y-1)2<2,对应的区域为以A为圆心半径为$\sqrt{2}$的圆及其内部,
作出对应的图象如图:
则弓形区域的面积S=$\frac{1}{4}×π•(\sqrt{2})^{2}-\frac{1}{2}×(\sqrt{2})^{2}$=$\frac{π}{2}-1=\frac{π-2}{2}$,
则对应的概率P=$\frac{\frac{π-2}{2}}{2×2}$=$\frac{π-2}{8}$,
故选:D
点评 本题主要考查几何概型的概率计算,根据条件求出对应区域的面积是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F1,作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
7.双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的左、右顶点分别为A1,A2,点P在C上且直线PA2的斜率的取值范围是($\frac{1}{2}$,1),那么直线PA1斜率的取值范围是( )
| A. | ($\frac{1}{3}$,$\frac{3}{4}$) | B. | ($\frac{3}{4}$,$\frac{5}{2}$) | C. | ($\frac{1}{3}$,$\frac{5}{2}$) | D. | ($\frac{5}{4}$,$\frac{5}{2}$) |
14.已知44(k)=36,把67转化为k进制数为( )
| A. | 55(k) | B. | 67(k) | C. | 103(k) | D. | 124(k) |
