题目内容
9.解不等式:100(1+x)20<120.分析 由100(1+x)20<120,得$(1+x)^{20}<\frac{6}{5}$,然后两边同时开20次方根求得|1+x|的范围,则不等式的解集可求.
解答 解:由100(1+x)20<120,得$(1+x)^{20}<\frac{6}{5}$,
即|1+x|$<\root{20}{\frac{6}{5}}$,解得:$-\root{20}{\frac{6}{5}}-1<x<\root{20}{\frac{6}{5}}-1$.
∴不等式100(1+x)20<120的解集为($-\root{20}{\frac{6}{5}}-1,\root{20}{\frac{6}{5}}-1$).
点评 本题考查不等式的解法,考查了有理指数幂的化简与求值,是基础题.

练习册系列答案
相关题目
4.阅读下面的流程图,若输入a=5,b=-1,则输出的a值为( )
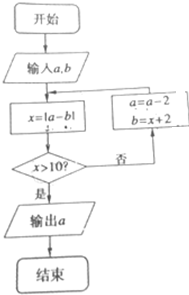

| A. | 16 | B. | 10 | C. | -3 | D. | -5 |
14.若x-y=2,x2+y2=4,则x2010+y2010的值为( )
| A. | -22010 | B. | 22010 | C. | 22010或-22010 | D. | 0 |
19.已知向量$\overrightarrow{OP}$=(1,1),$\overrightarrow{{OP}_{1}}$=(4,-4),且P2点分有向线段$\overrightarrow{P{P}_{1}}$所成的比为-2,则$\overrightarrow{{OP}_{2}}$的坐标是( )
| A. | (-$\frac{5}{2}$,$\frac{3}{2}$) | B. | ($\frac{5}{2}$,-$\frac{3}{2}$) | C. | (7,-9) | D. | (9,-7) |
 如图,正五边形ABCDE中,M为CD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,$\overrightarrow{DE}$=$\overrightarrow{d}$,试用$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AM}$和$\overrightarrow{BE}$.
如图,正五边形ABCDE中,M为CD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,$\overrightarrow{DE}$=$\overrightarrow{d}$,试用$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AM}$和$\overrightarrow{BE}$.