题目内容
7.已知{an}是递增的等差数列,a1=f(x),a2=4,a3=f(x+2),其中f(x)=x2+2(1)求数列{an}的前n项和Sn;
(2)令bn=$\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$+…+$\sqrt{{S}_{n}}$,[x]表示不超过x的最大整数(例如,[2.1]=2)
①分别写出[2$\sqrt{{S}_{1}}$],[$\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$]的值;
②令cn=[$\frac{2{b}_{n}}{n}$],求数列{cn}的通项公式.
分析 (1)由等差数列的性质结合已知列式求得x,则首项和公差可求,数列{an}的前n项和Sn可求;
(2)由$n=\sqrt{{n}^{2}}<\sqrt{n(n+1)}<\frac{1}{2}(2n+1)$,得到[$2\sqrt{{S}_{n}}$]=2n,同时得到$\frac{n(n+1)}{2}<\sqrt{{S}_{1}}+\sqrt{{S}_{2}}+…+\sqrt{{S}_{n}}<\frac{{n}^{2}+2n}{2}$.
①由新定义可得[2$\sqrt{{S}_{1}}$],[$\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$]的值;
②由$\frac{n(n+1)}{2}<\sqrt{{S}_{1}}+\sqrt{{S}_{2}}+…+\sqrt{{S}_{n}}<\frac{{n}^{2}+2n}{2}$求出2bn的范围,代入cn=[$\frac{2{b}_{n}}{n}$]可求数列{cn}的通项公式.
解答 解:(1)∵{an}是递增的等差数列,且a1=f(x),a2=4,a3=f(x+2),
∴f(x)+f(x+2)=8,即x2+2+(x+2)2+2=8,
解得:x=0或x=-2(舍).
∴a1=2,d=2,则${S}_{n}=2n+\frac{n(n-1)}{2}×2={n}^{2}+n$;
(2)∵$n=\sqrt{{n}^{2}}<\sqrt{n(n+1)}<\frac{1}{2}(2n+1)$,
∴$n<\sqrt{{S}_{n}}<n+\frac{1}{2}$,$2n<2\sqrt{{S}_{n}}<2n+1$,
则[$2\sqrt{{S}_{n}}$]=2n.
1+2+…+n$<\sqrt{{S}_{1}}+\sqrt{{S}_{2}}+…+\sqrt{{S}_{n}}<$1+2+…+n+$\frac{n}{2}$,
∴$\frac{n(n+1)}{2}<\sqrt{{S}_{1}}+\sqrt{{S}_{2}}+…+\sqrt{{S}_{n}}<\frac{{n}^{2}+2n}{2}$.
①[2$\sqrt{{S}_{1}}$]=2,[$\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$]=3;
②∵bn=$\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$+…+$\sqrt{{S}_{n}}$,
∴n(n+1)<2bn<n(n+2),
则n+1$<\frac{2{b}_{n}}{n}$<n+2.
∴cn=[$\frac{2{b}_{n}}{n}$]=n+1.
点评 本题是新定义题,考查数列的函数特性,考查了放缩法在解题中的应用,考查了学生的逻辑思维能力,难度较大.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | $\frac{b}{a}<1$ | C. | lg(a-b)>0 | D. | ${(\frac{1}{3})^a}<{(\frac{1}{3})^b}$ |
| A. | |a|=|b| | B. | a<0且a=-b | C. | a>0且a≠b | D. | a≤0 |
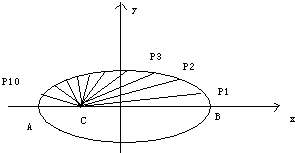 极坐标方程ρ=$\frac{ep}{1-ecosθ}$,(p>0,e>0),可以转化为平面直角坐标方程$\frac{{\sqrt{{x^2}+{y^2}}}}{{|{x+p}|}}$=e,该式子可以解释为:点(x,y)到原点的距离与到x=-p的距离之比为e,根据圆锥曲线的定义可以得到:ρ=$\frac{ep}{1-ecosθ}$表示一个以原点为其中一个焦点,以x=-p为对应准线的圆锥曲线.如图:过椭圆$\frac{x^2}{16}$+$\frac{y^2}{9}$=1的左焦点C作CP1,CP2,CP3…CP10等分∠ACB(A,B分别为椭圆的左右顶点),记P1,P2,P3…P10到左准线的距离分别为d1,d2,d3…d10,则$\frac{1}{d_1}$+$\frac{1}{d_2}$+$\frac{1}{d_3}$+…+$\frac{1}{{{d_{10}}}}$=$\frac{{10\sqrt{7}}}{9}$.
极坐标方程ρ=$\frac{ep}{1-ecosθ}$,(p>0,e>0),可以转化为平面直角坐标方程$\frac{{\sqrt{{x^2}+{y^2}}}}{{|{x+p}|}}$=e,该式子可以解释为:点(x,y)到原点的距离与到x=-p的距离之比为e,根据圆锥曲线的定义可以得到:ρ=$\frac{ep}{1-ecosθ}$表示一个以原点为其中一个焦点,以x=-p为对应准线的圆锥曲线.如图:过椭圆$\frac{x^2}{16}$+$\frac{y^2}{9}$=1的左焦点C作CP1,CP2,CP3…CP10等分∠ACB(A,B分别为椭圆的左右顶点),记P1,P2,P3…P10到左准线的距离分别为d1,d2,d3…d10,则$\frac{1}{d_1}$+$\frac{1}{d_2}$+$\frac{1}{d_3}$+…+$\frac{1}{{{d_{10}}}}$=$\frac{{10\sqrt{7}}}{9}$.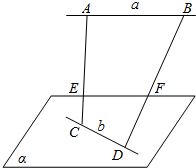 如图所示,a,b是异面直线,A,B∈a,C,D∈b,E,F分别为线段AC,BD的中点,判断直线EF和a的位置关系,并证明你的结论.
如图所示,a,b是异面直线,A,B∈a,C,D∈b,E,F分别为线段AC,BD的中点,判断直线EF和a的位置关系,并证明你的结论.