题目内容
设数集M同时满足条件①M中不含元素-1,0,1,②若a∈M,则
∈M.则下列结论正确的是( )
| 1+a |
| 1-a |
| A、集合M中至多有2个元素 |
| B、集合M中至多有3个元素 |
| C、集合M中有且仅有4个元素 |
| D、集合M中有无穷多个元素 |
考点:元素与集合关系的判断
专题:集合
分析:根据条件分别进行推理即可得到结论.
解答:解:若集合只含有一个元素,则
=a,即1+a=a-a2,
即-a2=1,不成立.
当a=3,则
=-2∈M
所以
=-
∈M
所以
=
∈M
所以,
=3
开始重复了,所以 M={3,-2,-
,
},
当a=2时,即2∈M,则
=-3∈M,
若-3∈M,则
=-
∈M,
若-
∈M,则
=
∈M,
若
∈M,有
=2∈M,
则A={2,-3,-
,-
},此时也只要四个元素,
根据归纳推理可得,集合M中有且仅有4个元素.
故选:C
| 1+a |
| 1-a |
即-a2=1,不成立.
当a=3,则
| 1+3 |
| 1-3 |
所以
| 1-2 |
| 1+2 |
| 1 |
| 3 |
所以
1-
| ||
1+
|
| 1 |
| 2 |
所以,
1+
| ||
1-
|
开始重复了,所以 M={3,-2,-
| 1 |
| 3 |
| 1 |
| 2 |
当a=2时,即2∈M,则
| 1+2 |
| 1-2 |
若-3∈M,则
| 1-3 |
| 1+3 |
| 1 |
| 2 |
若-
| 1 |
| 2 |
1-
| ||
1+
|
| 1 |
| 3 |
若
| 1 |
| 3 |
1+
| ||
1-
|
则A={2,-3,-
| 1 |
| 2 |
| 1 |
| 3 |
根据归纳推理可得,集合M中有且仅有4个元素.
故选:C
点评:本题主要考查命题的真假判断,利用元素和集合之间的关系是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目
对于任意两个正整数m,n,定义某种运算?:当m,n都为偶数或奇数时,m?n=m+n;当m,n中一个为奇数,另一个为偶数时,m?n=m•n.则在上述定义下,集合M={(x,y)|x?y=36,x∈N*,y∈N*}中元素的个数为( )
| A、48 | B、41 | C、40 | D、39 |
已知集合A={x∈Q|x>-1},B={x∈R|x<2},则下列说法正确的是( )
A、
| ||
| B、A∩B=(-1,2) | ||
| C、A∪B=R | ||
| D、1∈A∩B |
设集合N={x|x2≤x},则N=( )
| A、{0,1} | B、[0,1] | C、(0,1) | D、[0,1) |
集合{x∈N|-1≤x<5}用列举法表示为( )
| A、{0,1,2,3,4} | B、{-1,0,1,2,3,4} | C、{1,2,3,4} | D、{1,2,3,4,5} |
已知集合M={a,b,c},N={b,c,d},则( )
| A、M⊆N | B、N⊆M | C、M∩N={b,c} | D、M∪N={a,d} |
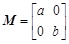 (其中
(其中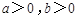 ),若曲线
),若曲线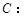
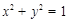 在矩阵
在矩阵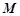 所对应的变换作用下得到曲线
所对应的变换作用下得到曲线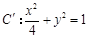 ,求
,求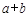 的值.
的值.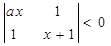 对任意
对任意 恒成立,则实数
恒成立,则实数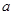 的取值范围是 .
的取值范围是 .