题目内容
已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+ =0相切。
=0相切。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交随圆C于另一点E,证明直线AE与x轴相交于定点Q;
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+ =0相切。
=0相切。(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交随圆C于另一点E,证明直线AE与x轴相交于定点Q;
:(Ⅰ)由题意知e=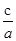 =
= ,所以e2=
,所以e2=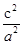 =
=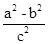 =
=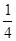 .即a2=
.即a2=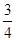 b2.
b2.
又因为b=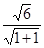 =
=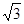 ,所以a2=4,b2=3.故椭圆的方程为
,所以a2=4,b2=3.故椭圆的方程为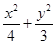 =1.…4分
=1.…4分
(Ⅱ)由题意知直线PB的斜率存在,设直线PB的方程为y=k(x-4),和椭圆方程联立解决.
由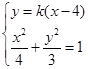 ,得(4k2+3)x2-32k2x+64k2-12=0. ①…6分
,得(4k2+3)x2-32k2x+64k2-12=0. ①…6分
设点B(x1,y1),E(x2,y2),则A(x1,-y1).直线AE的方程为y-y2=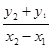 (x-x2).令y=0,得x=x2-
(x-x2).令y=0,得x=x2-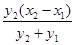 .将y1=k(x1-4),y2=k(x2-4)代入,
.将y1=k(x1-4),y2=k(x2-4)代入,
整理,得x=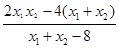 . ②…8分
. ②…8分
由①得x1+x2=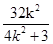 ,x1x2=
,x1x2=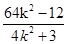 …10分 代入②整理,得x=1.
…10分 代入②整理,得x=1.
所以直线AE与x轴相交于定点Q(1,0)
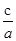 =
= ,所以e2=
,所以e2=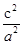 =
=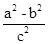 =
=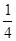 .即a2=
.即a2=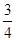 b2.
b2.又因为b=
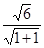 =
=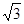 ,所以a2=4,b2=3.故椭圆的方程为
,所以a2=4,b2=3.故椭圆的方程为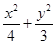 =1.…4分
=1.…4分(Ⅱ)由题意知直线PB的斜率存在,设直线PB的方程为y=k(x-4),和椭圆方程联立解决.
由
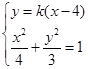 ,得(4k2+3)x2-32k2x+64k2-12=0. ①…6分
,得(4k2+3)x2-32k2x+64k2-12=0. ①…6分设点B(x1,y1),E(x2,y2),则A(x1,-y1).直线AE的方程为y-y2=
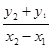 (x-x2).令y=0,得x=x2-
(x-x2).令y=0,得x=x2-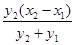 .将y1=k(x1-4),y2=k(x2-4)代入,
.将y1=k(x1-4),y2=k(x2-4)代入,整理,得x=
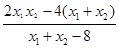 . ②…8分
. ②…8分由①得x1+x2=
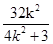 ,x1x2=
,x1x2=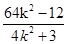 …10分 代入②整理,得x=1.
…10分 代入②整理,得x=1.所以直线AE与x轴相交于定点Q(1,0)
(1)离心率为 得
得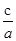 =
= ,椭圆的短半轴为半径的圆与直线x-y+
,椭圆的短半轴为半径的圆与直线x-y+ =0相切,b=
=0相切,b=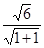 =
=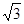 ,解得a2=4,b2=3;(Ⅱ)直线PB的方程为y=k(x-4)
,解得a2=4,b2=3;(Ⅱ)直线PB的方程为y=k(x-4)
 得
得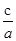 =
= ,椭圆的短半轴为半径的圆与直线x-y+
,椭圆的短半轴为半径的圆与直线x-y+ =0相切,b=
=0相切,b=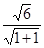 =
=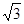 ,解得a2=4,b2=3;(Ⅱ)直线PB的方程为y=k(x-4)
,解得a2=4,b2=3;(Ⅱ)直线PB的方程为y=k(x-4)
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
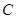 以
以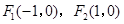 为焦点,且离心率
为焦点,且离心率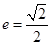 .
. 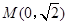 点斜率为
点斜率为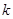 的直线
的直线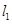 与椭圆
与椭圆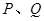 ,求
,求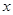 轴正半轴、
轴正半轴、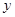 轴正半轴的交点分别为
轴正半轴的交点分别为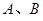 ,是否存在直线
,是否存在直线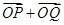 与
与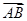 垂直?如果存在,写出
垂直?如果存在,写出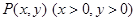 是双曲线
是双曲线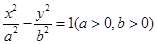 上的动点,
上的动点,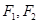 是双曲线的焦点,
是双曲线的焦点,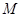 是
是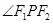 的平分线上一点,且
的平分线上一点,且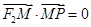 .某同学用以下方法研究
.某同学用以下方法研究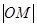 :延长
:延长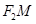 交
交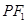 于点
于点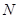 ,可知
,可知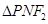 为等腰三角形,且
为等腰三角形,且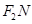 的中点,得
的中点,得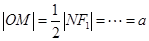 .类似地:点
.类似地:点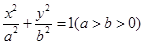 上的动点,
上的动点,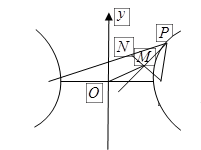
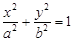 (a>b>0)的离心率为
(a>b>0)的离心率为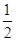 ,且经过点P(1,
,且经过点P(1,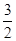 )。
)。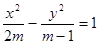 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线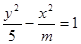 的离心率
的离心率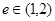 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。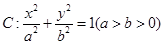 的离心率为
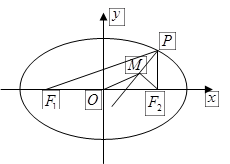
的离心率为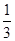 ,椭圆上的点到右焦点F的最近距离为2,若椭圆C与x轴交于A、B两点,M是椭圆C上异于A、B的任意一点,直线MA交直线
,椭圆上的点到右焦点F的最近距离为2,若椭圆C与x轴交于A、B两点,M是椭圆C上异于A、B的任意一点,直线MA交直线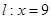 于G点,直线MB交直线
于G点,直线MB交直线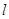 于H点。
于H点。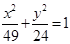 共焦点,且以
共焦点,且以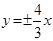 为渐近线,求双曲线方程.
为渐近线,求双曲线方程.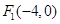 ,
,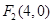 ,P在椭圆上,若 △
,P在椭圆上,若 △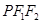 的面积的最大值为12,则椭圆方程为
的面积的最大值为12,则椭圆方程为



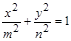 ,
,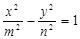 ,
,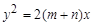 ,(其中
,(其中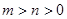 )的离心率分别为
)的离心率分别为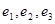 ,则( ).
,则( ).


 大小不确定
大小不确定