题目内容
定义在R上的函数f(x)满足:对任意实数m,n,总有f(m+n)=f(m)•f(n),且当x>0时,0<f(x)<1.
(1)试求f(0)的值;
(2)判断f(x)的单调性并证明你的结论;
(3)若对任意的t∈R,不等式f(t2-2t)-f(k-2t2)<0恒成立,求k的取值范围.
解:(1)在f(m+n)=f(m)•f(n)中令m=1,n=0,得:f(1)=f(1)•f(0)
因为f(1)≠0,所以,f(0)=1.
(2)要判断f(x)的单调性,可任取x1,x2∈R,且设x1<x2.
在f(m+n)=f(m)•f(n)中取m+n=x2,m=x1,
则f(x2)=f(x1)•f(x2-x1),
∵x2-x1>0,
∴0<f(x2-x1)<1
为比较f(x2),f(x1)的大小,只需考虑fx1( )的正负即可.
在在f(m+n)=f(m)•f(n)中令m=x,n=-x,则得f(x)-f(-x)=1.
∵x>0时0<f(x)<1,
∴当x<0时,f(x)=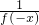 >1>0.
>1>0.
又f(0)=1,所以,综上,可知,对于任意x1∈R,均有f(x1)>0.
∴f(x2)-f(x1)=f(x1)[f(x2-x1)-1]<0.
∴函数f(x)在R上单调递减.
(3)不等式即f(t2-2t)<f(k-2t2),
由(2)知函数f(x)在R上单调递减,
∴t2-2t>k-2t2,
∴k<3t2-2t,其中t∈R.
∴k<(3t2-2t)min,而3t2-2t=3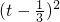 -
- ≤
≤ ,
,
∴k<- ,即k的取值范围是(-∞,-
,即k的取值范围是(-∞,- ).
).
分析:(1)在f(m+n)=f(m)•f(n)中令m=1,n=0,即可求得f(0)的值;
(2)要判断f(x)的单调性,可任取x1,x2∈R,且设x1<x2,可证得f(x2)-f(x1)<0,从而可判断f(x)的单调性;
(3)由(2)知,f(t2-2t)-f(k-2t2)<0恒成立?k<3t2-2t(t∈R)?k<(3t2-2t)min,从而可求k的取值范围.
点评:本题考查抽象函数及其应用,考查赋值法,考查函数单调性的判定,考查转化思想与方程思想,考查逻辑推理与综合应用能力,属于难题.
因为f(1)≠0,所以,f(0)=1.
(2)要判断f(x)的单调性,可任取x1,x2∈R,且设x1<x2.
在f(m+n)=f(m)•f(n)中取m+n=x2,m=x1,
则f(x2)=f(x1)•f(x2-x1),
∵x2-x1>0,
∴0<f(x2-x1)<1
为比较f(x2),f(x1)的大小,只需考虑fx1( )的正负即可.
在在f(m+n)=f(m)•f(n)中令m=x,n=-x,则得f(x)-f(-x)=1.
∵x>0时0<f(x)<1,
∴当x<0时,f(x)=
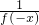 >1>0.
>1>0.又f(0)=1,所以,综上,可知,对于任意x1∈R,均有f(x1)>0.
∴f(x2)-f(x1)=f(x1)[f(x2-x1)-1]<0.
∴函数f(x)在R上单调递减.
(3)不等式即f(t2-2t)<f(k-2t2),
由(2)知函数f(x)在R上单调递减,
∴t2-2t>k-2t2,
∴k<3t2-2t,其中t∈R.
∴k<(3t2-2t)min,而3t2-2t=3
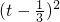 -
- ≤
≤ ,
,∴k<-
 ,即k的取值范围是(-∞,-
,即k的取值范围是(-∞,- ).
).分析:(1)在f(m+n)=f(m)•f(n)中令m=1,n=0,即可求得f(0)的值;
(2)要判断f(x)的单调性,可任取x1,x2∈R,且设x1<x2,可证得f(x2)-f(x1)<0,从而可判断f(x)的单调性;
(3)由(2)知,f(t2-2t)-f(k-2t2)<0恒成立?k<3t2-2t(t∈R)?k<(3t2-2t)min,从而可求k的取值范围.
点评:本题考查抽象函数及其应用,考查赋值法,考查函数单调性的判定,考查转化思想与方程思想,考查逻辑推理与综合应用能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目