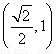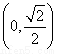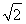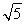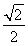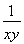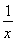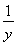题目内容
已知椭圆与双曲线x2－y2＝0有相同的焦点，且离心率为
.
(1)求椭圆的标准方程；
(2)过点P(0，1)的直线与该椭圆交于A，B两点，O为坐标原点，若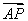
＝2
，求△AOB的面积．
（1）
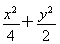＝1（2）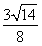
【解析】(1)设椭圆方程为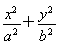
＝1，a>b>0，
由c＝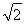
，
＝
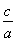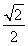，可得a＝2，b2＝a2－c2＝2，
所以椭圆的标准方程为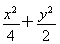＝1.
(2)设A(x1，y1)，B(x2，y2)，由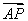
＝2
，得
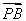可得x1＝－2x2.①
设过点P的直线方程为y＝kx＋1，代入椭圆方程，整理得(2k2＋1)x2＋4kx－2＝0，
则x1＋x2＝－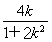
，②x1x2＝
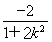，③
由①②得x2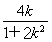＝，将x1＝－2x2代入③得
＝
，
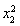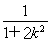所以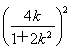
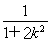＝，解得k2＝
.
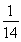又△AOB的面积S＝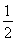
|OP|·|x1－x2|＝
·
＝
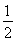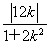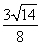.所以△AOB的面积是
.
练习册系列答案
相关题目
