题目内容
16.已知三个正数a,b,c满足a≤b+c≤3a,3b2≤a(a+c)≤5b2,则$\frac{b-2c}{a}$的最小值是( )| A. | -$\frac{18}{5}$ | B. | -3 | C. | 0 | D. | 不存在 |
分析 将不等式组进行转化,设$\frac{b}{a}$=x,$\frac{c}{a}$=y,利用线性规划的知识进行求解即可.
解答 解:不等式a≤b+c≤3a,3b2≤a(a+c)≤5b2,
等价为1≤$\frac{b}{a}$+$\frac{c}{a}$≤3,3($\frac{b}{a}$)2≤1+$\frac{c}{a}$≤5($\frac{b}{a}$)2,
设$\frac{b}{a}$=x,$\frac{b}{a}$=y,
则不等式等价为$\left\{\begin{array}{l}1≤x+y≤3\\ 3{x}^{2}≤1+y≤5{x}^{2}\\ x>0,y>0\end{array}\right.$,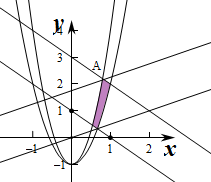
即$\left\{\begin{array}{l}x+y≥1\\ x+y≤3\\ y≥3{x}^{2}-1\\ y≤5{x}^{2}-1\\ x>0\\ y>0\end{array}\right.$,
则$\frac{b-2c}{a}$=$\frac{b}{a}$-2•$\frac{c}{a}$=x-2y,
设z=x-2y,
作出不等式组对应的平面区域如图:
由z=x-2y得y=$\frac{1}{2}$x-$\frac{1}{2}$z,
平移直线y=$\frac{1}{2}$x-$\frac{1}{2}$z,
由图象可知当直线y=$\frac{1}{2}$x-$\frac{1}{2}$z,过点A时,直线y=$\frac{1}{2}$x-$\frac{1}{2}$z的截距最大,此时z最小,
由$\left\{\begin{array}{l}x+y=3\\ y=5{x}^{2}-1\\ x>0\\ y>0\end{array}\right.$,解得x=$\frac{4}{5}$,y=$\frac{11}{5}$,
代入目标函数z=x-2y,
得z=-$\frac{18}{5}$
∴目标函数z=x-2y的最小值是-$\frac{18}{5}$,
故选:A
点评 本题主要考查线性规划的应用,将不等式组进行转化,利用换元法转化为线性规划的知识是解决本题的关键.综合性较强.

 阅读快车系列答案
阅读快车系列答案| A. | 4 | B. | 6 | C. | 9 | D. | $\frac{27}{2}$ |
| A. | 1 | B. | -1 | C. | $\sqrt{2}$ | D. | $-\sqrt{2}$ |
| A. | “至少有1名女生”与“都是女生” | B. | “至少有1名女生”与“至多1名女生” | ||
| C. | “恰有1名女生”与“恰有2名女生” | D. | “至少有1名男生”与“都是女生” |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
| A. | 2 | B. | 4 | C. | 3 | D. | $\sqrt{3}$ |