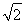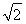题目内容
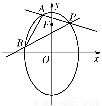
在平面直角坐标系xOy中，椭圆C的中心为原点，焦点F1，F2在x轴上，离心率为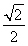
.过F1的直线l交C于A，B两点，且△ABF2的周长为16，那么C的方程为________．
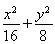=1
【解析】设椭圆方程为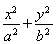
＝1(a＞b＞0)，
因为AB过F1且A，B在椭圆上，如图，
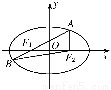
则△ABF2的周长为|AB|＋|AF2|＋|BF2|＝|AF1|＋|AF2|＋|BF1|＋|BF2|＝4a＝16，解得a＝4.
又离心率e＝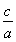
＝
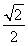，故c＝2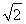
.
所以b2＝a2－c2＝8，所以椭圆C的方程为
＝1.
练习册系列答案
相关题目
某校为了研究学生的性别和对待某一活动的态度(支持和不支持的两种态度)的关系，运用2×2列联表进行独立性检验，经计算K2＝7.069，则所得到的统计学结论是：有________的把握认为“学生性别与支持该活动有关系”( )
附：
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
A.0.1% B．1% C．99% D．99.9%
