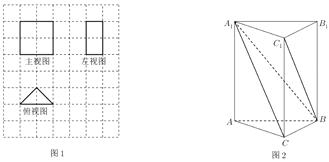
题目内容
【题目】设不等式![]() 表示的平面区别为
表示的平面区别为![]() .区域
.区域![]() 内的动点
内的动点![]() 到直线
到直线![]() 和直线
和直线![]() 的距离之积为2.记点
的距离之积为2.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .过点
.过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 垂直于
垂直于![]() 轴,
轴,![]() 为曲线
为曲线![]() 上一点,求
上一点,求![]() 的取值范围;
的取值范围;
(3)若以线段![]() 为直径的圆与
为直径的圆与![]() 轴相切,求直线
轴相切,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据“区域![]() 内的动点
内的动点![]() 到直线
到直线![]() 和直线
和直线![]() 的距离之积为
的距离之积为![]() ”列方程,化简后求得曲线
”列方程,化简后求得曲线![]() 的方程.
的方程.
(2)求得![]() 两点的坐标,利用平面向量数量积的坐标运算化简
两点的坐标,利用平面向量数量积的坐标运算化简![]() ,由此求得
,由此求得![]() 的取值范围.
的取值范围.
(3)设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和曲线
的方程和曲线![]() ,写出韦达定理.求得以
,写出韦达定理.求得以![]() 为直径的圆的圆心和直径,根据圆与
为直径的圆的圆心和直径,根据圆与![]() 轴相切列方程,解方程求得直线
轴相切列方程,解方程求得直线![]() 的斜率.
的斜率.
(1)设![]() ,依题意
,依题意![]() ①,因为
①,因为![]() 满足不等式
满足不等式![]() ,所以①可化为
,所以①可化为![]() .
.
(2)将![]() 代入曲线
代入曲线![]() 的方程
的方程![]() ,解得
,解得![]() .取
.取![]() ,设
,设![]() ,因为
,因为![]() 为曲线
为曲线![]() 上一点,故
上一点,故![]() .则
.则![]()
![]()
![]() .即
.即![]() 的取值范围是
的取值范围是![]() .
.
(3)设直线![]() 的方程是
的方程是![]() ,
,![]() .联立
.联立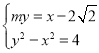 ,消去
,消去![]() 得
得![]() ,所以
,所以![]() .
.
设线段![]() 的中点为
的中点为![]() ,则
,则![]() ,所以
,所以 .
.![]()
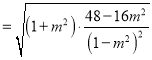 .因为以线段
.因为以线段![]() 为直径的圆与
为直径的圆与![]() 轴相切,所以
轴相切,所以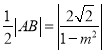 ,即
,即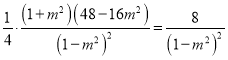 ,化简得
,化简得![]() .所以直线
.所以直线![]() 的斜率为
的斜率为![]() .
.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
【题目】某大学为调研学生在![]() ,
, ![]() 两家餐厅用餐的满意度,从在
两家餐厅用餐的满意度,从在![]() ,
, ![]() 两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以10为组距分成6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
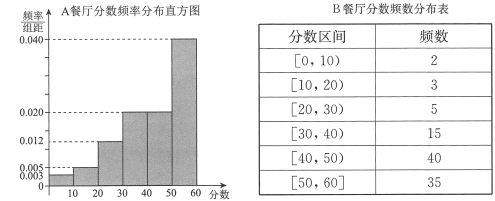
, ![]() ,得到
,得到![]() 餐厅分数的频率分布直方图,和
餐厅分数的频率分布直方图,和![]() 餐厅分数的频数分布表:
餐厅分数的频数分布表:
定义学生对餐厅评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 |
|
|
|
(Ⅰ)在抽样的100人中,求对![]() 餐厅评价“满意度指数”为0的人数;
餐厅评价“满意度指数”为0的人数;
(Ⅱ)从该校在, ![]() 两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对
两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对![]() 餐厅评价的“满意度指数”比对
餐厅评价的“满意度指数”比对![]() 餐厅评价的“满意度指数”高的概率;
餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从![]() ,
, ![]() 两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
两家餐厅中选择一家用餐,你会选择哪一家?说明理由.