题目内容
前12个正整数组成一个集合,此集合的符合如下条件的子集的数目为:子集均含有4个元素,且这4个元素至少有两个是连续的.则等于
| A.126 | B.360 | C.369 | D.495 |
C
专题:计算题.
分析:根据题意,首先分析可得:12个正整数中任取4个的取法数目,再用插空法计算其中任意两个数都不连续的子集个数,由间接法计算可得答案.
解答:解:根据题意,用间接法,
首先分析可得:12个正整数中任取4个,共
 =495种取法,
=495种取法,再计算其中任意两个数都不连续的子集个数,用插空法,除了已选的个元素外应有8个元素,这8个元素共9个空,9选4,插空,有一种插空的方法就有对应一种满足任意两个数都不连续
的抽取方法,则有
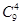 =126种;
=126种;则这4个元素至少有两个是连续的取法有
 -
-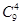 =495-126=369种;
=495-126=369种;故选C.
点评:本题考查排列、组合的综合运用,解题时注意这类问题的特殊方法的运用,如本题先用间接法,再用插空法解决不相邻问题.

练习册系列答案
相关题目
 ( )
( )

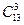
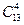
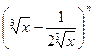 的展开式中,前三项系数的绝对值成等差数列.(12分)(1)求展开式的第四项;(2)求展开式的常数项;
的展开式中,前三项系数的绝对值成等差数列.(12分)(1)求展开式的第四项;(2)求展开式的常数项; 3,4的盒子内,则4号盒子中至少有一个球的放法有_______种(用数字作答).
3,4的盒子内,则4号盒子中至少有一个球的放法有_______种(用数字作答).