题目内容
10.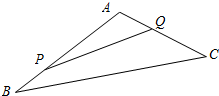 如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,造价均为每平方米100元.若围围墙用了20000元,问如何围可使竹篱笆用料最省?
分析 (1)设AP=x米,AQ=y米,则x+y=200,△APQ的面积S=$\frac{1}{2}$xysin120°=$\frac{\sqrt{3}}{4}$xy,利用基本不等式,可得结论;
(2)由题意得100×(x+1.5y)=20000,即x+1.5y=200,要使竹篱笆用料最省,只需PQ最短,利用余弦定理求出PQ,即可得出结论.
解答 解:设AP=x米,AQ=y米,则
(1)x+y=200,△APQ的面积S=$\frac{1}{2}$xysin120°=$\frac{\sqrt{3}}{4}$xy$≤\frac{\sqrt{3}}{4}•(\frac{x+y}{2})^{2}$=2500$\sqrt{3}$,
当且仅当x=y=100时取等号;
(2)由题意得100×(x+1.5y)=20000,即x+1.5y=200,
要使竹篱笆用料最省,只需PQ最短,所以
PQ2=x2+y2-2xycos120°=x2+y2+xy=(200-1.5y)2+y2+(200-1.5y)y
=1.75y2-400y+40000(0<y<$\frac{400}{3}$)
所以y=$\frac{800}{7}$时,PQ有最小值$\frac{200\sqrt{21}}{7}$,此时x=$\frac{200}{7}$.
点评 本题考查利用数学知识解决实际问题,考查三角形面积的计算,余弦定理的运用,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5.函数y=2sin$\frac{x}{2}$+1的图象的一条对称轴方程是( )
| A. | x=$\frac{π}{2}$+1 | B. | x=$\frac{π}{2}$ | C. | x=π+1 | D. | x=π |
 已知直二面角α-l-β,点A∈α,AC⊥l,C为垂足,点B∈α,BD⊥l,D为垂足,若AB=2,AC=BD=1,求D到平面ABC的距离.
已知直二面角α-l-β,点A∈α,AC⊥l,C为垂足,点B∈α,BD⊥l,D为垂足,若AB=2,AC=BD=1,求D到平面ABC的距离.