题目内容
2.已知集合A={x|x2+mx+2m<0},B={x|x2-4≤0},若A⊆B,求m的取值范围.分析 先求出集合B={x|-2≤x≤2},可设f(x)=x2+mx+2m,讨论判别式△:△≤0时,f(x)≥0,得到A=∅,符合A⊆B;△>0时,m需满足$\left\{\begin{array}{l}{f(-2)≥0}\\{f(2)≥0}\\{-2<-\frac{m}{2}<2}\end{array}\right.$,这样求出每种情况下m的取值范围再求并集即可.
解答 解:B={x|-2≤x≤2};
设f(x)=x2+mx+2m;
①若△=m2-8m≤0,即0≤m≤8,f(x)≥0,∴A=∅,满足A⊆B;
②若△>0,即m<0,或m>8;
要使A⊆B,则:
$\left\{\begin{array}{l}{f(-2)=4-2m+2m≥0}\\{f(2)=4+4m≥0}\\{-2<-\frac{m}{2}<2}\end{array}\right.$;
解得-1≤m<4;
∴此时-1≤m<0;
综上得m的取值范围为[-1,8].
点评 考查描述法表示集合,解一元二次不等式,判别式△的取值和二次函数取值的关系,可借助二次函数的图象.

练习册系列答案
相关题目
12.x是三角形的一个内角,且sinx+cosx=-$\frac{1}{5}$,则tanx的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
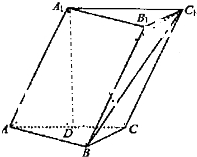 如图,三棱锥ABC-A1B1C1的底面ABC是正三角形,A1D⊥平面ABC,D是AC的中点.
如图,三棱锥ABC-A1B1C1的底面ABC是正三角形,A1D⊥平面ABC,D是AC的中点.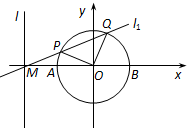 已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).
已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).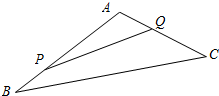 如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆. 如图所示,设抛物线y2=2px与圆(x-5)2+y2=16在x轴上方的交点为A和B,线段AB的中点C(4,yC)
如图所示,设抛物线y2=2px与圆(x-5)2+y2=16在x轴上方的交点为A和B,线段AB的中点C(4,yC)